C++11 Template (模板编程)

C++ Template

模板基础

函数模板

定义模板

template <typename T>
inline T const& tmax(T const& a, T const& b)
{
    return a < b ? b: a;
}

使用模板

1	max(32, 43);

通常而言，并不是把模板编译成一个可以处理任何类型的单一实体。
而是对于实例化模板参数的每种类型，都从模板产生一个不同的实体。
这种用具体类型代替模板参数的过程叫做实例化，它产生了一个模板的实例。

由此，我们可以得出一个结论：模板被编译了两次，分别发生在：

实例化之前，先检查模板代码本身，查看语法是否正确；在这里会发现错误的语法，如遗漏分号等。
在实例化期间，检查模板代码，查看是否所有的调用都有效。在这里会发现无效的调用，如该实例化类型不支持某些函数调用(该类型没有提供模板所需要使用到的操作)等。

实参的演绎（deduction）

模板实参不允许进行自动类型转换；每个T都必须正确地匹配。

1	max(4, 4.3); // Error:第1个参数类型是int，第2个参数类型是double

模板参数

函数模板有两种类型的参数

模板参数：位于函数模板名称的前面，在一对尖括号内部进行声明：

1	template <typename T> // T是模板参数

调用参数：位于函数模板名称之后，在一对圆括号内部进行声明：

1	...max(T const& a, T const& b); // a和b都是调用参数

函数模板和类模板区别：

函数模板可以进行模板实参演绎(不能演绎返回类型)、重载、指定缺省调用实参、全局特化；~~不能指定缺省模板实参~~(已经可以了)，~~不能局部特化~~；类模板可以指定缺省模板实参、指定全局特化和局部特化(用来完成类似函数模板重载功能)；不能重载类模板，不能进行实参演绎。

显式实例化：

当模板参数和调用参数没有发生关联，或者不能由调用参数来决定模板参数的时候，在调用时就必须显式指定模板实参。切记，模板实参演绎并不适合返回类型。如下

1	template <typename T1, typename T2, typename RT>
2	inline RT max(T1 const& a, T2 const& b);

那么必须进行显式实例化：

1	max<int, double, double>(4, 4.3); // OK，但很麻烦。这里T1和T2是不同的类型，所以可以指定两个不同类型的实参4和4.3

通常而言，你必须指定“最后一个不能被隐式演绎的模板实参之前的”所有实参类型。上面的例子中，改变模板参数的声明顺序，那么调用者就只需要指定返回类型：

1	template <typename RT, typename T1, typename T2>
2	inline RT max(T1 const& a, T2 const& b);
3	...
4	max<double>(4, 4.3); // ok，返回类型是double

重载函数模板

对于非模板函数和同名的函数模板，如果其他条件都是相同的话，那么在调用的时候，重载解析过程通常会优先调用非模板函数，而不会从该模板产生出一个实例。然而，如果模板可以产生一个具有更好匹配的函数，那么将选择模板。
可以显式地指定一个空的模板实参列表，这个语法好像是告诉编译器：只有模板才能匹配这个调用（即便非模板函数更符合匹配条件也不会被调用到），而且所有的模板参数都应该根据调用实参演绎出来。
因为模板是不允许自动类型转化的；但普通函数可以进行自动类型转换，所以当一个匹配既没有非模板函数，也没有函数模板可以匹配到的时候，会尝试通过自动类型转换调用到非模板函数（前提是可以转换为非模板函数的参数类型）
在所有重载的实现里面，我们都是通过引用来传递每个实参的。一般而言，在重载函数模板的时候，最好只是改变那些需要改变的内容；就是说，你应该把你的改变限制在下面两种情况：改变参数的数目或者显式地指定模板参数。否则可能会出现非预期的结果。
定义一个重载函数A，而在A1(函数A的重载)中调用A，但是，如果直到A1的定义处还没有见到A的定义(也即函数A的定义在函数A1的后面，但函数A1中调用了函数A)，那么并不会调用到这个重载函数A，而会寻找在函数A1之前已经定义了的符合条件的其他函数Ax（即便A是符合条件的非模板函数，而Ax是模板函数，也会由于A的声明太迟，而选择调用Ax）

类模板

类模板的Stack实现

#include <cassert>
#include <vector>

template <typename T>
class Stack {
private:
	std::vector<T> elems;  // elements

public:
	void push(T const& elem);  // push element
	void pop();                // pop element
	T const& top() const;      // return top element
	bool empty() const {       // return whether the stack is empty
		return elems.empty();
	}
};

template <typename T>
void Stack<T>::push(T const& elem) {
	elems.push_back(elem);  // append copy of passed elem
}

template <typename T>
void Stack<T>::pop() {
	assert(!elems.empty());
	elems.pop_back();  // remove last element
}

template <typename T>
T const& Stack<T>::top() const {
	assert(!elems.empty());
	return elems.back();  // return copy of last element
}

这个类的类型是Stack<T>,其中T是模板参数。因此，当在声明中需要使用该类的类型时，你必须使用Stack<T>。然而，当使用类名而不是类的类型时，就应该只用Stack;譬如，当你指定类的名称、类的构造函数、析构函数时，就应该使用Stack

为了定义类模板的成员函数，必须指定该成员函数是一个函数模板，而且你还需要使用这个类模板的完整类型限定符

显然，对于类模板的任何成员函数，你都可以把它实现为内联函数，将它定义于类声明里面，如：

template <typename T>
class Stack
{
    ...
    void push(T const& elem)
    {
        elems.push_back(elem);
    }
    ...
};

类模板Stack的使用

为了使用类模板对象，必须显式地指定模板实参。

只有那些被调用的成员函数，才会产生这些函数的实例化代码。
对于类模板，成员函数只有在被使用的时候才会被实例化。显然，这样可以节省空间和时间；
另一个好处是，对于那些“未能提供所有成员函数中所有操作的”类型，你也可以使用该类型来实例化类模板，只要对那些“未能提供某些操作的”成员函数，模板内部不使用就可以。
如果类模板中含有静态成员，那么用来实例化的每种类型，都会实例化这些静态成员。

切记，要作为模板参数类型，唯一的要求就是：该类型必须提供被调用的所有操作。

类模板的特化

为了特化一个类模板，你必须在起始处声明一个__template<>__，接下来声明用来特化类模板的类型。这个类型被用作模板实参，且必须在类名的后面直接指定：

template<>
class Stack<std::string>
{
    ...
};

进行类模板的特化时，每个成员函数都必须重新定义为普通函数，原来模板函数中的每个T也相应地被进行特化的类型取代。如:

1	void Stack<std::string>::push(std::string const& elem)
2	{
3	elems.push_back(elem);
4	}

局部特化

1	// 两个模板参数具有相同的类型
2	template <typename T>
3	class Myclass<T, T> //
4	{
5	};
6
7	// 第2个模板参数的类型是int
8	template <typename T>
9	class Myclass<T, int>
10	{
11	};
12
13	// 两个模板参数都是指针类型
14	template <typename T1, typename T2>
15	class Myclass<T1, T2> // 也可以使引用类型T&，常引用等
16	{
17	};

局部特化种类1：把模板类型列表里，部分的类型，特化。

template<typename T, typename M> class test{
    T i;
    M m;
};
template<typename M> class test<bool, M>{
    int i;
};

上面的例子，把类型T特化了，类型M保留了，所以是部分特化。也就是当外部使用时，穿进来的T的类型是bool类型的话，就进入到特化定义的类里。

局部特化种类2：限定泛化类型，比如限定成指针。

template<typename T> class test{
    T i;
};
template<typename T> class test<T*>{
    T i;
};
template<typename T> class test<const T*>{
    T i;
};

上面的例子，把类型限定了，如果外部穿进来的是指针则有特殊的处理，如果穿进来的是const指针，则有另外的特殊处理。

缺省模板实参

对于类模板，你还可以为模板参数定义缺省值；这些值就被称为缺省模板实参；而且它们还可以引用之前的模板参数。(STL容器使用缺省默认实参指定内存分配其alloc)如：

template <typename T, typename CONT = std::vector<T> >
class Stack
{
};

template <typename T1, typename T2  = int>
class Sample
{
};

非类型模板参数

非类型的类模板参数:

template <typename T, int MAXSIZE>
class Stack
{
};
// 使用
Stack<int, 20> int20Stack;     // 可以存储20个int元素的栈
Stack<int, 40> int40Stack;     // 可以存储40个int元素的栈 

每个模板实例都具有自己的类型，因此int20Stack和int40Stack属于不同的类型，而且这两种类型之间也不存在显式或者隐式的类型转换；所以它们之间不能互相替换，更不能互相赋值。

然而，如果从优化设计的观点来看，这个例子并不适合使用缺省值。缺省值应该是直观上正确的值。但对于栈的类型和大小而言，int类型和最大容量100从直观上看起来都不是正确的。因此，在这里最好还是让程序员显式地指定这两个值。因此我们可以在设计文档中用一条声明来说明这两个属性（即类型和最大容量）。

非类型的函数模板参数:

template <typename T, int VAL>
T addValue(T const& x)
{
   return x + VAL;
} 

借助标准模板库（STL）使用上面例子：

1	std::transform(source.begin(), source.end(), dest.begin(), addValue<int, 5>);

上面的调用中，最后一个实参实例化了函数模板addValue()，它让int元素增加5.
这个例子有一个问题：addValue<int, 5>是一个函数模板实例，而函数模板实例通常被看成是用来命名一组重载函数的集合（即使该组只有一个函数）。
然而，根据现今的标准，重载函数的集合并不能被用于模板参数的演绎（注意，标准模板库中的函数是使用模板定义的，故而在transform()函数中，参数是作为函数模板调用实参传递的，也即参与了模板参数演绎）。于是，必须将这个函数模板的实参强制类型转换为具体的类型：

1	std::transform(source.begin(), source.end(), dest.begin(), (int(*)(int const&))addValue<int, 5>);

非类型模板参数的限制:

非类型模板参数是有限制的。
通常而言，它们可以是常整数（包括枚举值）或者指向外部链接对象的指针。
注：浮点数和类对象（class-type)是不允许作为非类型模板参数的。

之所以不能使用浮点数（包括简单的常量浮点表达式）作为模板实参是有历史原因的。然而以后可能会支持这个特性。
另外，由于字符串文字是内部链接对象（因为两个具有相同名称但出于不同模块的字符串，是两个完全不同的对象），所以你不能使用它们来作为模板实参

template <char const* name>
class MyClass
{
};
MyClass<"hello"> x;   // ERROR:不允许使用字符文字"hello"
//另外，你也不能使用全局指针作为模板参数：
template <char const* name>
class MyClass
{
    ...
};
char const* s = "hello";
MyClass<s> x;   // s是一个指向内部链接对象的指针
//然而，你可以这样使用：
template <char const* name>
class MyClass
{
    ...
};
extern char const s[] = "hello";
MyClass<s> x;   // OK
//全局字符数组s由“hello”初始化，是一个外部链接对象。

技巧性基础知识

关键字typename:

C++标准化过程中，引入关键字typename是为了说明：模板内部的标识符可以是一个类型。

template <typename T>
class MyClass
{
    // 这里的typename被用来说明：T::SubType是定义于类T内部的一种类型
    typename T::SubType* ptr;
    ...
};

使用this->

考虑例子

template <typename T>
class Base
{
    public:
        void exit();
};

template <typename T>
class Derived : Base<T>    // 模板基类
{
    public:
        void foo()
        {
             exit();    // 调用外部的exit()或者出现错误，而不会调用模板基类的exit()
        }
};

对于那些在基类中声明，并且依赖于模板参数的符号（函数或者变量等），你应该在它们前面使用this->或者Base::限定符。如果希望完全避免不确定性，你可以（使用诸如this->和Base::等）限定（模板中）所有的成员访问。（这两种限定符的详细信息会在本系列文章后面讲解）

成员模板

对于类模板而言，其实例化只有在类型完全相同才能相互赋值。我们通过定义一个身为模板的赋值运算符（成员模板），来达到两个不同类型（但类型可以转换）的实例进行相互赋值的目的，如下声明：

template <typename T>
class Stack
{
    ...
    template <typename T2>
        Stack<T>& operator= (Stack<T2> const&);
};

模板的模板参数

还是以Stack为例：

template <typename T,
                template <typename ELEM,
                                    typename ALLOC = std::allocator<ELEM> >
                                        class CONT = std::deque >
class Stack
{
    ...
};

上面作为模板参数里面的class 不能用typename代替；
还有一个要知道：函数模板并不支持模板的模板参数。
之所以需要定义“ALLOC”，是因为模板的模板实参“std::deque”具有一个缺省模板参数，为了精确匹配模板的模板参数；

零初始化

对于int、double或者指针等基本类型，并不存在“用一个有用的缺省值来对它们进行初始化”的缺省构造函数；相反，任何未被初始化的局部变量都具有一个不确定值。如果我们希望我们的模板类型的变量都已经用缺省值初始化完毕，那么针对内建类型，我们需要做一些处理。

1	// 函数模板
2	template <typename T>
3	void foo()
4	{
5	T x = T(); // 如果T是内建类型，x是0或者false
6	}；
7	// 类模板：初始化列表来初始化模板成员
8	template <typename T>
9	class MyClass
10	{
11	private:
12	T x;
13	public:
14	MyClass() : x() {} // 确认x已被初始化，内建类型对象也是如此
15	};

使用字符串作为函数模板的实参

有时，把字符串传递给函数模板的引用参数会导致出人意料的运行结果。

1	#include <string>
2	// 注意，method1:引用参数
3	template <typename T>
4	inline T const& max(T const& a, T const& b)
5	{
6	return a < b ? b : a;
7	}
8
9	//method2:非引用参数
10	template <typename T>
11	inline T max2(T a, T b)
12	{
13	return a < b ? b : a;
14	}
15
16	int main()
17	{
18	std::string s;
19	// 引用参数
20	::max("apple", "peach"); // OK, 相同类型的实参
21	::max("apple", "tomato"); // ERROR, 不同类型的实参
22	::max("apple", s); // ERROR, 不同类型的实参
23	// 非引用参数
24	::max2("apple", "peach"); // OK, 相同类型的实参
25	::max2("apple", "tomato"); // OK, 退化(decay)为相同类型的实参
26	::max2("apple", s); // ERROR, 不同类型的实参
27	}

method1的问题在于：由于长度的区别，这些字符串属于不同的数值类型。也就是说，“apple”和“peach”具有相同的类型char const[6]；然而“tomato”的类型则是char const[7]。

method2调用正确的原因是：对于非引用类型的参数，在实参演绎的过程中，会出现数组到指针的类型转换（这种转型通常也被称为decay）。

小结：
如果遇到一个关于字符数组和字符指针之间不匹配的问题，你会意外地发现和这个问题会有一定的相似之处。这个问题并没有通用的解决方法，根据不同情况，可以：

使用非引用参数，取代引用参数（然而，这可能会导致无用的拷贝）；
进行重载，编写接收引用参数和非引用参数的两个重载函数（然而，这可能会导致二义性）；
对具体类型进行重载（譬如对std::string进行重载）；
重载数组类型，譬如

template <typename T, int N, int M>
T const* max (T const (&a)[N], T const (&b)[M])
{
    return a < b ? b : a;
}

强制要求应用程序程序员使用显式类型转换。
对于当前的例子，最好的方法是为字符串重载max().无论如何，为字符串提供重载都是必要的，否则比较的将是两个字符串的地址。

模板术语

类模板__还是__模板类

在C++中，类和联合（union）都被称为类类型（class type）。如果不加额外的限定，我们通常所说的“类（class）”是指：用关键字class或者struct引入的类类型。需要特别注意的一点就是：类类型包括联合，而“类”不包括联合。

实例化__和__特化

模板实例化是一个通过使用具体值替换模板实参，从模板产生出普通类、函数或者成员函数的过程。这个过程最后获得的实体（譬如类、函数或成员函数）就是我们通常所说的特化。
然而，在C++中，实例化过程并不是产生特化的唯一方式。程序员可以使用其他机制来显式地指定某个声明，该声明对模板参数进行特定的替换，从而产生特化

template <typename T1, typename T2>     // 基本的类模板
class MyClass
{
    ...
};
template<>    // 显式特化
class MyClass<std::string, float>
{
    ...
};

上面就是我们通常所讲的显式特化（区别于实例化特化或者其他方式产生的特化）。

template <typename T>     // 基本的类模板
class MyClass<T, T>
{
    ...
};
template<typename T>    // 局部特化
class MyClass<bool, T>
{
    ...
};

当谈及（显式或隐式）特化的时候，我们把普通模板称为基本模板。

深入模板基础

参数化声明

函数模板和类模板：

// 类模板
template <typename T>
class List      // 作为名字空间作用域的类模板
{
    public:
        template <typename T2>
        List(List<T2> const&);     // 成员函数模板（构造函数）
};

template <typename T>
    template <typename T2>
List<T>::List(List<T2> const& b){} // 位于类外部的成员函数模板定义

// 位于外部名字空间作用域的函数模板
template <typename T>
int length(List<T> const&);

// 联合（Union）模板，往往被看作类模板的一种
template <typename T>
union AllocChunk
{
    T object;
    usigned char bytes[sizeof(T)];
};

两种基本类型的模板之外，还可以使用相似的符号来参数化其他的3种声明。这3种声明分别都有与之对应的类模板成员的定义：

类模板的成员函数的定义；
类模板的嵌套类成员的定义；
类模板的静态数据成员的定义；

template <int I>
class CupBoard
{
    void open();
    class Shelf;
    static double total_weight;
    ...
};

template <int I>
void CupBoard<I>::open(){ ... }

template <int I>
class CupBoard<I>::Shelf { ... };

template <int I>
double CupBoard<I>::total_weight = 0.0;

Template parameters may be of any of the three kinds of C++ entities: values, types, or templates:

1	template <int N> struct Foo; // N is a value
2	template <typename T> struct Bar; // T is a type
3	template <template <typename> class X> struct Zip; // X is a template

usage:

1	Foo<10> a;
2	Bar<int> b;
3	Zip<Bar> c;

Note that this corresponds to the three ways of disamiguating dependent names:

1	X::a = 10; // X::a is a value
2	typename X::B n = 10; // X::B is a type
3	X::template C<int> m; // X::C is a template

虚成员函数

成员函数模板不能被声明为虚函数。
这是一种需要强制执行的限制，因为虚函数调用机制的普遍实现都使用了一个大小固定的表，每个虚函数都对应表的一个入口。然而，成员函数模板的实例化个数，要等到整个程序都翻译完毕才能确定，这就和表的大小（是固定的）发生了冲突。如果（将来）要支持虚成员函数模板，将需要一种全新的C++编译器和链接器机制。

类模板的普通成员可以是虚函数，因为当类被实例化之后，它们的个数是固定的：

template <typename T>
class Dynamic
{
    public:
        virtual ~Dynamic();      // ok：类模板的普通成员函数，每个Dynamic只对应一个析构函数
        template <typename T2>
        virtual void copy(T2 const&);     // 错误，在确定Dynamic<T>实例的时候，并不知道copy()的个数
};

模板的链接

每个模板都必须有一个名字，而且在它所属的作用域下，该名字必须是唯一的；除非函数模板可以被重载。特别是，类模板不能和另外一个实体共享一个名称，这一点和class类型是不同的

int C;
class C;       // 正确：类名称和非类名称位于不同的名字空间

int X;
template <typename T>
class X;        //Error: Redefinition of 'X' as different kind of symbol

struct S;
template <typename T>
class S;           //Error：Redefinition of 'S' as different kind of symbol

模板名字是具有链接的，当它们不能具有C链接

extern "C++" template <typename T>
void normal();        // 这是缺省情况，上面的链接规范可以不写

extern "C" template <typename T> // ERROR: Templates must have C++ linkage
void invalid();

extern "Xroma" template <typename T>
void xroma_link();        // 非标准的，当某些编译器将来可能支持写Xroma语言的链接兼容性

模板通常具有外部链接，唯一的例外就是__前面有static修饰符的名字空间作用域下的函数模板__：

1	// 作为一个声明，引用位于其他文件的、具有相同名称的实体；即引用位于其他文件的external()函数模板，也称前置声明
2	template <typename T>
3	void external();
4
5	// 与其他文件中具有相同名称的模板没有关系，即不是外部链接
6	template <typename T>
7	static void internal();

因此我们知道（由于外部链接）：不能在函数内部声明模板。

基本模板

如果模板声明的是一个普通声明，我们就称它声明的是一个基本模板。这类模板声明是指：没有在模板名称后面添加一对尖括号（和里面实参）的声明

1	template <typename T> class Box;
2	template <typename T> void translate(T*);

显然，当声明局部特化的时候，声明的就是非基本模板。另外，函数模板必须是基本模板。

模板参数

存在3种模板参数：

类型参数
类型参数是通过关键字typename或者class引入的:它们两者几乎是等同的。在模板声明内部，类型参数的作用类似于typedef（类型定义）名称。例如，如果T是一个模板参数，就不能使用诸如class T 等形式的修饰名称，即使T是一个要被class类型替换的参数也不可以。
非类型参数
非类型参数表示的是：在编译期或链接期可以确定的常值。这种参数的类型必须是下面的一种
1. 整型或者枚举类型
2. 指针类型（包含普通对象的指针类型、函数指针类型、指向成员的指针类型）
3. 引用类型（指向对象或者指向函数的引用都是允许的)
函数和数值类型也可以被指定为非模板参数，但要把它们先隐式地转换为指针类型，这种转型也称为decay:
1
template <int buf[5]> class Lexer; // buf实际上是一个int*类型
2
template <int* buf> class Lexer; // 正确：这是上面的重新声明
非类型模板参数的声明和变量的声明很相似，但它们不能具有static、mutable等修饰符；只能具有const和volatile限定符。但如果这两个限定符限定的如果是最外层的参数类型，编译器将会忽略它们：
1
template <int const length> class Buffer; // 这里的const是没用的，被忽略了
非类型模板参数只能是右值：它们不能被取址，也不能被赋值。
模板的模板参数
模板的模板参数是代表类模板的占位符（placeholder）。它的声明和类模板的声明很类似，但不能使用关键字struct和union：

1	template <template<typename X> class C>
2	void f(C<int>* p);

对于模板的模板参数而言，它的参数名称只能被自身其他参数的声明使用。

模板实参

模板实参是指：在实例化模板时，用来替换模板参数的值。下面几种机制可以来确定这些值：

显式模板实参：紧跟在模板名称后面，在一对尖括号内部的显式模板实参值。所组成的整个实体称为template-id。
注入式(injecter)类名称：对于具有模板参数P1、P2……的类模板X，在它的作用域中，模板名称（即X）等同于template-id：X<P1, P2, ……>。
缺省模板实参：如果提供缺省模板实参的话，在类模板的实例中就可以省略显式模板实参。然而，即使所有的模板参数都具有缺省值，一对尖括号还是不能省略的（即使尖括号内部为空，也要保留尖括号）。
实参演绎：对于不是显式指定的函数模板实参，可以在函数的调用语句中，根据函数调用实参的类型来演绎出函数模板实参。

函数模板实参

显式指定或者实参演绎。

对于某些模板实参永远也得不到演绎的机会（比如函数返回值类型）。于是我们最好把这些实参所对应的参数放在模板参数列表的开始处（为了显式指定模板参数T，需要把T放到参数列表最前；为了提供T的缺省模板实参，需要确保参数列表中位于T后面的模板参数也都提供了缺省实参），从而可以显式指定这些参数，而其他参数仍可以进行实参演绎

template <typename RT, typename T>
inline RT func(T const &){ ... }

template <typename T, typename RT>
inline RT func1(T const &){ ... }

int main()
{
    double value1 = func<double>(-1);   // double 显式指定RT类型，-1实参演绎T类型
    double value2 = func1<int, double>(-1);   // 要显式指定RT的类型，必须同时显式指定它前面的类型T
}

类型实参

模板的类型实参是一些用来指定模板类型参数的值。我们平时使用的大多数类型都可以被用作模板的类型实参。但有两种情况例外：

局部类和局部枚举（换句话说，指在函数定义内部声明的类型）不能作为模板的类型实参；
未命名的class类型或者未命名的枚举类型不能作为模板的类型实参（然而，通过typedef声明给出的未命名类和枚举是可以作为模板类型实参的）

template <typename T> class List
{
    ...
};

typedef struct
{
    double x, y, z;
}Point;

typedef enum { red, green, blue } *ColorPtr;

int main()
{
    struct Association
    {
        int* p;
        int* q;
    };

	 // 错误：模板实参中使用了局部类型
    List<Association*> error1;

	// 错误：模板实参中使用了未命名的类型，因为typedef定义的是*ColorPtr，并非ColorPtr
    List<ColorPtr> error2;

	 // 正确：通过使用typedef定义的未命名类型
    List<Point> ok;
}

非类型实参

非类型模板实参是那些替换非类型参数的值。这个值必须是以下几种中的一种：

某一个具有正确类型的非类型模板参数；
一个编译期整型常值（或枚举值）；这只有在参数类型和值的类型能够进行匹配，或者值的类型可以隐式地转换为参数类型的前提下，才是合法的。
前面有单目运算符&（即取址）的外部变量或者函数的名称。对于函数或数组变量，&运算符可以省略。这类模板实参可以匹配指针类型的非类型参数。
对于引用类型的非类型模板参数，前面没有&运算符的外部变量和外部函数也是可取的；
一个指向成员的指针常量；换句话说，类似&C::m的表达式，其中C是一个class类型，m是一个非静态成员（成员变量或者函数）。这类实参只能匹配类型为“成员指针”的非类型参数。

当实参匹配“指针类型或者引用类型的参数”时，用户定义的类型转换（例如单参数的构造函数和重载类型转换运算符）和由派生类到基类的类型转换，都是不会被考虑的;即使在其他的情况下，这些隐式类型指针是有效的，但在这里都是无效的。隐式类型转换的唯一应用只能是：给实参加上关键字const或者volatile。

1	template <typename T, T nontyep_param>
2	class C;
3
4	C<int, 33>* c1; // 整型
5
6	int a;
7	C<int, &a> c2; // 外部变量的地址
8
9	void f();
10	void f(int);
11	C<void()(int), f> c3; // 函数名称：在这个例子中，重载解析会选择f(int)，f前面的&隐式省略了
12
13	class X
14	{
15	public:
16	int n;
17	static bool b;
18	};
19
20	C<bool&, X::b>* c4; // 静态成员是可取的变量（和函数）名称
21
22	C<int X::, &X::n> c5; // 指向成员的指针常量
23
24	template<typename T>
25	void templ_func();
26
27	C<void(), &templ_func<double> >* c6; // 函数模板实例同时也是函数

模板实参的一个普遍约束是：在程序创建的时候，编译器或者链接器要能够确定实参的值。如果实参的值要等到程序运行时才能够确定（譬如，局部变量的地址），就不符合“模板是在程序创建的时候进行实例化”的概念了。（模板实参是一个在编译期可以确定的值，这样才符合“模板是在程序创建的时候进行实例化”的概念。）

另一方面，有些常值不能作为有效的非类型实参：空指针常量、浮点型值、字符串。

template <typename T, T nontyep_param>
class C;

class Base
{
    public:
        int i;
}base;

class Derived:public Base
{
}derived_obj;

C<Base*, &derived_obj>* err1;       // 错误：这里不会考虑派生类到基类的类型转换

C<int&, base.i>* err2;          // 错误：域运算符（.）后面的变量不会被看成变量

int a[10];
C<int*, &a[10]>* err3;      // 错误：单一数组元素的地址并不是可取的
C<int*, a>* ok;

模板特化

重载函数模板

template <typename T>
int f(T)
{
    return 1;
}

template <typename T>
int f(T*)
{
    return 2;
}

如果我们用int*来替换第1个模板的T，用int来替换第2个模板的T，那么将会获得两个具有相同参数类型（和返回类型）的同名函数。也就是说，不仅是同名模板可以同时存在，同名各自的实例化体也可以同时存在，即使这些实例化体具有相同的参数类型和返回类型。可以如下调用：

1	f<int>((int)0); //ouputs 1
2	f<int>((int*)0); //outpus 2

调用f<int*>((int*)0)。语法f<int*>说明我们希望用int来替换模板f的第1个模板参数，而且这种替换并不依赖于模板实参演绎。在这个例子中，有两个f模板，因此所生成的重载集包含了两个函数：f<int>(int*)（生成自第1个模板）和f<int*>(int**)（生成自第2个模板）。然而，调用实参(int*)0的类型是int*，因此它将会和第1个模板生成的函数更好地匹配，最后也就调用这个函数。类似的分析也可以用于第2个调用。

显式特化（全局特化）

类模板和函数模板都可以被全局特化；
类模板能局部特化，不能被重载；
函数模板能被重载，不能被局部特化。

特化具有对函数模板进行重载的这种能力，再加上可以利用局部排序规则选择最佳匹配的函数模板，我们就能够给泛型实现添加更加特殊的模板，从而可以透明地获得具有更高效率的代码。

然而，类模板不能被重载；我们可以选择另一种替换的机制来实现这种透明自定义类模板的能力，那就是显式特化。C++标准的“显式特化”概念指的是一种语言特性，我们通常也称之为全局特化。它为模板提供了一种使模板参数可以被全局替换的实现，而没有剩下模板参数。

事实上，类模板和函数模板都是可以被全局特化的，而且类模板的成员（包括成员函数、嵌入类、静态成员变量等，它们的定义可以位于类定义的外部）也可以被全局特化。

局部特化和全局特化有些类似，但局部特化并没有替换所有的模板参数，就是说某些参数化实现仍然保留在模板的（另一种）实现中。实际上，全局特化和局部特化都没有引入一个全新的模板或者模板实例。它们只是对原来的泛型（或者非特化）模板中已经隐式声明的实例提供另一种定义。在概念上，这是一个相对比较重要的现象，也是特化区别于重载模板的关键之处。

全局的类模板特化

template<typename T>
class S
{
    public:
        void info()
        {
            std::cout << "generic (S<T>::info() \n)";
        }
};

template<>
class S<void>
{
    public:
        void msg()
        {
            std::cout << "fully specialized (S<void>::msg()) \n";
        }
};

全局特化的实现不需要与（原来的）泛型实现有任何关联，这就允许我们可以包含不同名称的成员函数（info相对msg）。实际上，全局特化只和类模板的名称有关联。
指定的模板实参列表必须和相应的模板参数列表一一对应。例如，我们不能用一个非类型值来替换一个模板类型参数。然而，如果模板参数具有缺省模板实参，那么用来替换的模板实参就是可选的（即不是必须的）。

1	template<typename T>
2	class Types
3	{
4	public:
5	typedef int I;
6	};
7
8	template<typename T, typename U = typename Types<T>::I>
9	class S; // (1)
10
11	template<>
12	class S<void> // (2)
13	{
14	public:
15	void f();
16	};
17
18	template<> class S<char, char>; // (3)
19
20	template<> class S<char, 0>; // 错误：不能用0来替换U
21
22	int main()
23	{
24	S<int>* pi; // 正确：使用（1），这里不需要定义
25	S<int> e1; // 错误：使用（1），需要定义，但找不到定义
26
27	S<void>* pv; // 正确：使用（2）
28
29	S<void, int> sv; // 正确：使用（2），这里定义是存在的，因为模板特化的第2个参数的缺省类型为int类型
30	S<void, char> e2; // 错误：使用（1），需要定义，但找不到定义
31
32	S<char, char> e3; // 错误：使用（3），需要定义，但找不到定义
33	}
34
35	template<>
36	class S<char, char> // (3)处的定义
37	{
38	};

可见，（模板）全局特化的声明并不一定是定义。另外，当一个全局特化声明之后，针对该（特化的）模板实参列表的调用，将不再使用模板的泛型定义，而是使用这个全局特化的定义。因此，如果在调用处需要该特化的定义，而在这之前并没有提供这个定义，那么程序将会出现错误。对于类模板特化而言，“前置声明”类型有时候是很有用的，因为这样就可以构造相互依赖的类型。另外，以这种方式获得的全局特化声明（应该记住它并不是模板声明）和普通的类声明是类似的，唯一的区别在于语法以及该特化的声明必须匹配前面的模板声明。对于特化声明而言，因为它并不是模板声明，所以应该使用（位于类外部）的普通成员定义语法，来定义全局类模板特化的成员（也就是说，不能指定template<>前缀）：

template<typename T>
class S;

template<>
class S<char**>
{
    public:
        void print() const;
};

// 下面的定义不能使用template<>前缀
void S<char**>::print() const
{
    std::cout << "pointer to pointer to char \n";
}

全局的函数模板特化

就语法及其后所蕴涵的原则而言，（显式的）全局函数模板特化和类模板特化大体上是一致的，唯一的区别在于：函数模板特化引入了重载和实参演绎这两个概念。借助实参演绎（用实参类型来演绎声明中给出的参数类型）来确定模板的特殊化版本，那么全局特化就可以不声明显式的模板实参。

注意：全局函数模板特化不能包含缺省的实参值。然而，对于基本（即要被特化的）模板所指定的任何缺省实参，显式特化版本都可以应用这些缺省实参值。

1	template<typename T>
2	int f(T, T x = 42)
3	{
4	return x;
5	}
6
7	template<>
8	int f(int, int = 35) // 错误，不能包含缺省实参值,但如果没有指定第2个实参，则会使用基本模板的缺省参数值
9	{
10	return 0;
11	}
12
13	template<typename T>
14	int g(T, T x = 42)
15	{
16	return x;
17	}
18
19	template<>
20	int g(int, int y)
21	{
22	return y/2;
23	}
24
25	int main()
26	{
27	std::cout << g(0) << std::endl; // 正确，输出21
28	}

全局成员特化

除了成员模板之外，类模板的成员函数和普通的静态成员变量也可以被全局特化；实现特化的语法会要求给每个外围类模板加上template<>前缀。如果要对一个成员模板进行特化，也必须加上另一个template<>前缀，来说明该声明表示的是一个特化。为了说明这些含义，让我们假设具有下面的声明：

template<typename T>
class Outer      // (1)
{
    public:
        template<typename U>
        class Inner         // (2)
        {
            private:
                static int count;      // (3)
        };
        static int code;         // (4)
        void print() const      // (5)
        {
            std::cout << "generic";
        }
};

template<typename T>
int Outer<T>::code = 6;        // (6)

template<typename T>
    template<typename U>
int Outer<T>::Inner<U>::count = 7;       // (7)

template<>
class Outer<bool>         // (8)
{
    public:
        template<typename U>
        class Inner       // (9)
        {
            private:
                static int count;         // (10)
        };
    void print() const {}             // (11)
};

在（1）处的泛型模板Outer中，（4）处的code和（5）处print()，这两个普通成员都具有一个外围类模板。因此，需要使用一个template<>前缀说明：后面将用一个模板实参集来对它进行全局特化：

template<>
int Outer<void>::code = 12;

template<>
void Outer<void>::print() const
{
    std::cout << "Outer<void>";
}

这些定义将会用于替代类Outer在（4）处和（5）处的泛型定义；但是，类Outer的其他成员仍然默认地产生自（1）处的模板。另外，在提供了上面的声明之后，就不能再次提供Outer的显式特化。

类似于全局函数模板特化，我们需要一种可以在不指定定义的前提下（为了避免多处定义），可以声明类模板普通成员特化的。尽管对于普通类的成员函数和静态成员变量而言，非定义的类外声明在C++中是不允许的；但如果是针对类模板的特化成员，该声明则是合法的。也就是说，前面的定义可以具有如下声明:

template<>
int Outer<void>::code;

template<>
void Outer<void>::print() const;

动多态和静多态

多态是一种能够令单一的泛型标记关联不同特定行为的能力。在C中，多态主要是通过继承和虚函数来实现的。由于这两个机制（继承和虚函数）都是（至少一部分）在运行期进行处理的，因此我们把这种多态称为动多态；我们平常所谈论的C多态指的就是这种动多态。然而，模板也允许我们使用单一的泛型标记，来关联不同的特定行为；但这种（借助于模板的）关联是在编译期进行处理的，因此我们把这种（借助于模板的）多态称为静多态，从而和上面的动多态区分开来。

动多态

使用继承和虚函数，在这种情况下，多态的设计思想主要在于：对于几个相关对象的类型，确定它们之间的一个共同功能集；然后在基类中，把这些共同的功能声明为多个虚函数接口。每个具体类都派生自基类，生成了具体对象之后，客户端代码就可以通过指向基类的引用或指针来操作这些对象，并且能够通过这些引用或者指针来实现虚函数的调度机制。也就是说，利用一个指向基类（子对象）的指针或者引用来调用虚成员函数，实际上将可以调用（指针或者引用实际上所代表的）具体类对象的相应成员。这种动多态是C++程序设计里面最常见的，这里不过多的阐述。

静多态

模板也能够被用于实现多态


#include <vector>
#include "coord.hpp"

// 具体的几何对象类Circle
// - 并没有派生自任何其他的类
class Circle
{
    public:
        void draw() const;
        Coord center_of_gravity() const;
        ...
};

// 具体的几何对象类Line
// - 并没有派生自任何其他的类
class Line
{
    public:
        void draw() const;
        Coord center_of_gravity() const;
        ...
};

// 画出任意GeoObj
// method2
template <typename GeoObj>
void myDraw(GeoObj const& obj)     // GeoObj是模板参数
{
    obj.draw();      // 根据对象的类型调用相应的draw()
}

// method1:如果使用动多态，myDraw函数会是如下形式：
void myDraw(GeoObj const& obj)      // GeoObj是一个抽象基类
{
    obj.draw();
}

int main()
{
    Line l;
    Circle c;

    myDraw(l);         // myDraw<Line>(GeoObj&) => Line::draw()
    myDraw(c);         // myDraw<Circle>(GeoObj&) => Circle::draw()
}

比较myDraw()的两个实现，主要的区别在于method2的GeoObj的规范是模板参数，而不是一个公共基类。

使用动多态（method1），我们在运行期只具有一个myDraw()函数，
使用模板，我们则可能具有多个不同的函数，诸如myDraw()和myDraw()。

trait与policy类

模板让我们可以针对多种类型对类和函数进行参数，但我们并不希望为了能够最大程度地参数化而引入太多的模板参数，同时在客户端指定所有的相应实参往往也是烦人的。我们希望引入的大多数额外参数都具有合理的缺省值。在某些情况下额外参数还可以有几个主参数来确定。

policy类和trait（或者称为trait模板）是两种C++程序设计机制。它们有助于对某些额外参数的管理，
这里的额外参数是指：在具有工业强度的模板设计中所出现的参数。

trait类：提供所需要的关于模板参数的类型的所有必要信息；(STL源码大量运用了这种技巧)
policy类：有点像策略模式，通过policy类挂接不同的算法；

fixed traits

针对每个typename T类型都创建一个关联，所关联的类型就是用来存储累加和的类型。这种关联可以被看作是类型T的一个特征，因此，我们也把这个存储累加和的类型称为T的trait。于是，我们可以导出我们的第一个trait类：

template<typename T>
class AccumulationTraits;

template<>
class AccumulationTraits<char>
{
    public:
        typedef int AccT;
};

template<>
class AccumulationTraits<char>
{
    public:
        typedef int AccT;
};

template<>
class AccumulationTraits<short>
{
    public:
        typedef int AccT;
};

template<>
class AccumulationTraits<int>
{
    public:
        typedef long AccT;
};

template<>
class AccumulationTraits<unsigned int>
{
    public:
        typedef unsigned long AccT;
};

template<>
class AccumulationTraits<float>
{
    public:
        typedef double AccT;
};

在上面代码中，模板AccumulationTraits被称为一个trait模板，因为它含有它的参数类型的一个trait（通常而言，可以存在多个trait和多个参数）。对这个模板，我们并不提供一个泛型的定义，因为在我们不知道参数类型的前提下，并不能确定应该选择什么样的类型作为和的类型。然而，我们可以利用某个实参类型，而T本身通常都能够作为这样的一个候选类型。这样，我们可以改写accum()模板如下：

//ordinary version
template <typename T>
inline
T accum(T const* beg, T const* end)
{
    T total  = T();      // 假设T()事实上会产生一个等于0的值
    while(beg != end)
    {
        total += *beg;
        ++beg;
    }
    return total;
}

//trait version
template<typename T>
inline
typename AccumulationTraits<T>::AccT accum(T const* beg, T const* end)
{
    // 返回值的类型是一个元素类型的trait
    typedef typename AccumulationTraits<T>::AccT Acct;

    AccT total = AccT();        // 假设AccT()实际上生成了一个0值
    while(beg != end)
    {
        total += *beg;
        ++beg;
    }
    return total;
}

// 于是，现在例子程序的输入完全符合我们的期望，如下：
the average value of the integer values is 3
the average value of the characters in "templates" is 108

value trait

到目前为止，我们已经看到了trait可以用来表示：“主”类型所关联的一些额外的类型信息。在这一小节里，我们将阐明这个额外的信息并不局限于类型，常数和其他类型的值也可以和一个类型进行关联。

我们前面的accum()模板使用了缺省构造函数的返回值来初始化结果变量（即total），而且我们期望该返回值是一个类似0的值：

1	AccT total = AccT(); // 假设AccT()实际上生成了一个0值
2	...
3	return total;

显然，我们并不能保证上面的构造函数会返回一个符合条件的值，可以用来开始这个求和循环。而且，类型AccT也不一定具有一个缺省构造函数。

在此，我们可以再次使用trait来解决这个问题。对于上面的例子，我们需要给AccumulationTraits添加一个value trait

1	template<typename T>
2	class AccumulationTraits;
3
4	template<>
5	class AccumulationTraits<char>
6	{
7	public:
8	typedef int AccT;
9	// 之所以选择使用静态函数返回一个值，原因如下：
10	// 方案1: 直接定义“static AccT const zero = 0;”，
11	// 缺点: 在所在类的内部，C++只允许我们对整型和枚举类型初始化成静态成员变量
12	// 方案2: 类内声明“static double const zero;”
13	// 源文件进行初始化“double const AccumulationTraits<float>::zero = 0.0;”，
14	// 缺点: 这种解决方法对编译器而言是不可知的。
15	// 在处理客户端文件的时候，编译器通常都不会知道位于其他文件的定义
16	// 综上，选择了下面使用静态函数返回所需要的值的方法
17	static AccT zero(){
18	return 0;
19	}
20	};
21	// 其他内建类型的特化版本类似
22	......

对于应用程序代码而言，唯一的区别只是这里使用了函数调用语法（而不是访问一个静态数据成员）：

1	AccT total = AccumulationTraits<T>::zero();

显然，trait还可以代表更多的类型。在我们的例子中，trait可以是一个机制，用于提供accum()所需要的、关于元素类型的所有必要信息；实际上，这个元素类型就是调用accum()的类型，即模板参数的类型。下面是trait概念的关键部分：trait提供了一种配置具体元素（通常是类型）的途径，而该途径主要是用于泛型计算。

在上一节所使用的trait被称为fixed trait，因为一旦定义了这个分离的trait，就不能再算法中对它进行改写。然而，在有些情况下我们需要对trait进行改写。从原则上讲，参数化trait主要的目的在于：添加一个具有缺省值的模板参数，而且该缺省值是由我们前面介绍的trait模板决定的。在这种具有缺省值的情况下，许多用户就可以不需要提供这个额外的模板实参；但对于有特殊需求的用户，也可以改写这个预设的类型。

对于这个特殊的解决方案，唯一的不足在于：我们并不能对函数模板预设缺省模板实参。可以通过把算法实现为一个类，绕过这个不足。这同时也说明了：除了函数模板之外，在类模板中也可以很容易地使用trait，唯一的确点就是：类模板不能对它的模板参数进行演绎，而是必须显式提供这些模板参数。因此，我们需要编写如下形式的代码： Accum::accum(&name[0], &name[length]) 前面例子的代码修改如下：

template <typename T,
                typename AT = AccumulationTraits<T> >
class Accum
{
    public:
        static typename AT::AccT accum(T const* beg, T const* end)
        {
            typename AT::AccT total = AT::zero();
            while (beg != end)
            {
                total += *beg;
                ++beg;
            }
            return total;
        }
};

通常而言，大多数使用这个模板的用户都不必显式地提供第2个模板实参，因为我们可以针对第1个实参的类型，为每种类型都配置一个合适的缺省值。
和大多数情况一样，我们可以引入一个辅助函数，来简化上面基于类的接口：

template<typename T>
inline
typename AccumulationTraits<T>::AccT accum(T const* beg, T const* end)
{
    // 第2个实参由类模板的缺省实参提供
    return Accum<T>::accum(beg, end);
}

template<typename Traits, typename T>
inline
typename Traits<T>::AccT accum(T const* beg, T const* end)
{
    // 第2个实参由Traits实参提供，替换缺省实参
    return Accum<T, Traits>::accum(beg, end);
}

policy 和 policy类

到目前为止，我们把累积（accumulation）与求和（summation）等价起来了。事实上，还可以有其他种类的累积。例如，我们可以对序列中的给定值进行求积；如果这些值是字符串的话，还可以对它们进行连接。甚至于在一个序列中找到一个最大值，也可以被看成是累积问题的一种形式。

在这所有的情况中，针对accum()的所有操作，唯一需要改变的只是“total += *beg;” 操作。于是，我们就把这个操作称为该累积过程的一个policy。

因此，一个policy类就是一个提供了一个接口的类，该接口能够在算法中应用一个或多个policy。

policy，核心操作的一个代理，通过替换policy，达到改变算法核心操作，从而改变算法行为的目的

#include "accumtraits4.hpp"
#include "sumpolicy1.hpp"

template <typename T,
                typename Policy = SumPolicy,
                typename Traits = AccumulationTraits<T> >
class Accum
{
    public:
        typedef typename Traits::AccT AccT;
        static AccT accum(T const* beg, T const* end)
        {
            AccT total = Traits::zero();
            while (beg != end)
            {
                Policy::accumulate(total, *beg);
                ++beg;
            }
            return total;
        }
};

其中SumPolicy类可以编写如下：

class SumPolicy
{
    public:
        template<typename T1, typename T2>  // 成员模板
        static void accumulate(T1& total, T2 const & value)
        {
            total += value;
        }
};

在这个例子中，我们把policy实现为一个具有一个成员函数模板的普通类（也就是说，类本身不是模板，而且该成员函数是隐式内联的）。后面我们还会讨论另一种实现方案。
通过给累积值指定一个不同的policy，我们就可以进行不同的计算。如下：

#include <iostream>

class MultiPolicy
{
    public:
        template<typename T1, typename T2>
        static void accumulate(T1& total, T2 const & value){
            total *= value;
        }
};

int main()
{
    // 创建含有具有5个整型值的数组
    int num[] = {1, 2, 3, 4, 5};
    // 输出所有值的乘积
    std::cout << "the product of the integer values is " 
	              << Accum<int,MultiPolicy>::accum(&num[0], &num[5]) << std::endl;
}
// 程序的输出结果却出乎我们意料：
the product of the integer values is 0

显然，这里的问题是我们对初始值的选择不当所造成的：因为对于求和，0是一个合适的初值；但对于求积，0却是一个错误的初值。可以在policy实现zero()的trait，也可以把这个初值作为参数传递进来。

trait和policy

大多数人接受Andrei Alexandrescu在Modern C++ Design中给出的声明：

policyhe trait具有许多共同点，但是policy更加注重于行为，而trait则更加注重于类型。

此外，作为引入了trait技术的第1人，Nathan Myers给出了下面这个更加开放的定义：

trait class:是一种用于代替模板参数的类。
作为一个类，它可以是有用的类型，也可以是常量；
作为一个模板，它提供了一种实现“额外层次间接性”的途径，而正是这种“额外层次间接性”解决了所有的软件问题。

因此，我们通常会使用下面这些（并不是非常准确的）定义：

trait表述了模板参数的一些自然的额外属性；
policy表述了泛型函数和泛型类的一些可配置行为（通常都具有被经常使用的缺省值）。

为了更深入地分析这两个概念之间可能的区别，我们给出下面针对trait的一些事实：

trait可以是fixed trait（也就是说，不需要通过模板参数进行传递的trait）。
trait参数通常都具有很自然的缺省值（该缺省值很少会被改写的，或者是不能被改写的）。
trait参数可以紧密依赖于一个或多个主参数。
trait通常都是用trait模板来实现的。

对于policy class，我们将会发现下列事实：

如果不以模板参数的形式进行传递的话，policy class几乎不起作用。
policy 参数并不需要具有缺省值，而且通常都是显式指定这个参数（尽管许多泛型组件都配置了使用频率很高的缺省policy）。
policy参数和属于同一个模板的其他模板参数通常都是正交的。
policy class一般都包含了成员函数。
policy既可以用普通类来实现，也可以用类模板来实现。

成员模板和模板的模板参数

为了实现一个累积policy，在前面我们选择把Sumpolicy和MutPolicy实现为具有成员模板的普通类。
另外，还存在另一种实现方法，即使用类模板来设计这个policy class接口，而这个policy class也就被用作模板的模板实参。如下：

template <typename T1, typename T2>
class SumPolicy
{
    public:
        static void accumulate (T1& total, T2 const & value)
    {
        total += value;
    }
};

于是，可以对Accum的接口进行修改，从而使用一个模板的模板参数，如下：

template <typename T,
            // 模板的模板参数一般不会在类里面使用到，故而可以匿名
            template<typename, typename> class Policy = SumPolicy,
            typename Traits = AccumulationTraits<T> >
class Accum
{
    public:
        typedef typename Traits::AccT AccT;
        static AccT accum(T const* beg, T const* end)
    {
        AccT total = Traits::zero();
        while (beg != end)
        {
            Policy<AccT, T>::accumulate(total, *beg);
            ++beg;
        }
        return total;
    }
};

我们也可以不把AccT类型显式地传递给policy类型，而是只传递上面的累积trait，并且根据这个trait参数来确定返回结果的类型，而且这样做在某些情况下（诸如需要给trait其他的一些信息）是有利的。

通过模板的模板参数访问policy class的主要优点在于：

借助于某个依赖于模板参数的类型，就可以很容易地让policy class携带一些状态信息（也就是静态成员变量）。

而在我们的第1种解决方案中，却不得不把静态成员变量嵌入到成员类模板中。
然而，这种利用模板的模板参数的解决方案也存在一个缺点：

policy类现在必须被写成模板，而且我们的接口中还定义了模板参数的确切个数。
遗憾的是，这个定义会让我们无法在policy中添加额外的模板参数。
例如，我们希望给SumPolicy添加一个Boolean型的非类型模板实参，从而可以选择是用 += 运算符来进行求和，还是只用 + 运算符来进行求和。

组合多个policie和/或 trait

从我们上面的开发过程可以看出，trait和policy通常都不能完全代替多个模板参数；
然而，trait和policy确实可以减少模板参数的个数，并把个数限制在可控制的范围以内。

一种简单的策略就是根据缺省值使用频率递增地对各个参数进行排序。
显然，这意味着：trait参数将位于policy参数的后面（即右边），因为我们在客户端代码中通常都会对policy参数进行改写。

模板与继承

许多模板技术往往让类模板拖着一长串类型参数；不过许多参数都设有合理的缺省值，如：

template <typename policy1 = DefaultPolicy1,
                typename policy2 = DefaultPolicy2,
                typename policy3 = DefaultPolicy3,
                typename policy4 = DefaultPolicy4>
class BreadSlicer
{
    .......
};

一般情况下使用缺省模板实参BreadSlicer<>就足够了。不过，如果必须指定某个非缺省的实参，还必须明白地指定在它之前的所有实参（即使这些实参正好是缺省类型，也不能偷懒）。跟BreadSlicer<DefaultPolicy1, DefaultPolicy2, Custom>相比，BreadSlicer<Policy3 = Custom>显然更有吸引力

我们的考虑主要是设法将缺省类型值放到一个基类中，再根据需要通过派生覆盖掉某些类型值。这样，我们就不再直接指定类型实参了，而是通过辅助类完成。如BreadSlicer<Policy3_is<Custom>>。既然用辅助类做模板参数，每个辅助类都可以描述上述4个policy中的任意一个，故所有模板参数的缺省值均相同：

template <typename PolicySetter1 = DefaultPolicyArgs,
                typename PolicySetter2 = DefaultPolicyArgs,
                typename PolicySetter3 = DefaultPolicyArgs,
                typename PolicySetter4 = DefaultPolicyArgs>
class BreadSlicer
{
    typedef PolicySelector<PolicySetter1, PolicySetter2,
                                     PolicySetter3, PolicySetter4>
                Policies;
    // 使用Policies::P1, Policies::P2, ……来引用各个Policies
};

剩下的麻烦事就是实现模板PolicySelector。

这个模板的任务是利用typedef将各个模板实参合并到一个单一的类型（即Discriminator），该类型能够根据指定的非缺省类型（如policy1-is的Policy），改写缺省定义的typedef成员（如Default Policies的DefaultPolicy1）。其中合并的事情可以让继承来干

// PolicySelector<A, B, C, D>生成A, B, C, D作为基类
// Discriminator<>使Policy Selector可以多次继承自相同的基类
// PolicySelector不能直接从Setter继承
template <typename Base, int D>
class Discriminator : public Base{
};

template <typename Setter1, typename Setter2,
                typename Setter3, typename Setter4>
class PolicySelector : public Discriminator<Setter1, 1>,
                                public Discriminator<Setter2, 2>,
                                public Discriminator<Setter3, 3>,
                                public Discriminator<Setter4, 4>{
};

由于中间模板Discriminator的引入，我们就可以一致处理各个Setter类型（不能直接从多个相同类型的基类继承，但可以借助中间类间接继承）。
如前所述，我们还需要把缺省值集中到一个基类中：

// 分别命名缺省policies为P1, P2, P3, P4
class DefaultPolicies
{
    public:
        typedef DefaultPolicy1 P1;
        typedef DefaultPolicy2 P2;
        typedef DefaultPolicy3 P3;
        typedef DefaultPolicy4 P4;
};

不过由于会多次从这个基类继承，我们必须小心以避免二义性，故用虚拟继承：

1	// 一个为了使用缺省policy值的类
2	// 如果我们多次派生自DefaultPolicies，下面的虚拟继承就避免了二义性
3	class DefaultPolicyArgs : virtual public DefaultPolicies{
4	};

最后，我们只需要写几个模板覆盖掉缺省的policy参数：

template <typename Policy>
class Policy1_is : virtual public DefaultPolicies
{
    public:
        typedef Policy P1;           //改写缺省的typedef
};

template <typename Policy>
class Policy2_is : virtual public DefaultPolicies
{
    public:
        typedef Policy P2;           //改写缺省的typedef
};

template <typename Policy>
class Policy3_is : virtual public DefaultPolicies
{
    public:
        typedef Policy P3;           //改写缺省的typedef
};

template <typename Policy>
class Policy4_is : virtual public DefaultPolicies
{
    public:
        typedef Policy P4;           //改写缺省的typedef
};

最后，我们把模板BreadSlicer实例化为：

1	BreadSlicer<Policy3_is<CustomPolicy> > bc;

这时模板BreadSlicer中的类型Polices被定义为：

1	PolicySelector<Policy3_is<CustomPolicy>,
2	DefaultPolicyArgs,
3	DefaultPolicyArgs,
4	DefaultPolicyArgs>

所有的模板实参都是基类，而它们有共同的虚基类DefaultPolicies，正是这个共同的虚基类定义了P1, P2, P3和P4的缺省类型；不过，其中一个派生类Policy3_is<>重定义了P3。根据优势规则，重定义的类型隐藏了基类中的定义，这里没有二义性问题。

模板元编程

meta programming含有“对一个程序进行编程”的意思。换句话说，编程系统将会执行我们所写的代码，来生成新的代码，而这些新代码才真正实现了我们所期望的功能。通常而言，meta programming这个概念意味着一种反射的特性：metaprogramminig组件只是程序的一部分，而且它也只生成一部分代码或者程序。

使用metaprogramming的目的是为了实现更多的功能，并且是花费的开销更小。
另一方面，metaprogramming的最大特点在于：某些用户自定义的计算可以在程序翻译期进行。而这通常都能够在性能或接口简单性方面带来好处；甚至为两方面同时带来好处。

递归模板

模板实例化机制是一种基本的递归语言机制，可以用于在编译期执行复杂的计算。因此，这种随着模板实例化所出现的编译期计算通常就被称为template meta programming。

如何在编译期计算3的幂

// 用于计算3的N次方的基本模板
template <int N>
class Pow3
{
    public:
        enum { result = 3 * Pow3<N-1>::result };
};

// 用于结束递归的全局特化
template<>
class Pow3<0>
{
    public:
        enum { result = 1 };
};

//斐波拉切数列
template <int N>
struct Factorial
{
    static const int value = N * Factorial<N-1>::value; // recursive!
};

template <> // template specialisation
struct Factorial<0> // required for terminating condition
{
    static const int value = 1;
};

Pow3<>模板（包含它的特化）就被称为一个template metaprogramming。它描述一些可以在翻译期（编译期）进行求值的计算，而这整个求值过程属于模板实例化过程的一部分。

枚举值 VS 静态常量

静态成员变量只能是左值，若编译器将必须传递Pow3<7>::result的地址，便会强制编译器实例化静态成员的定义，并为该定义分配内存。于是，该计算将不再局限于完全的“编译期”效果。然而，枚举值却不是左值（也就是说，它们并没有地址）。因此，当你通过引用传递枚举值的时候，并不会使用任何静态内存，就像是以文字常量的形式传递这个完成计算的值一样。所以，下面的所有例子，我们使用枚举值而不是静态常量。

表达式模板

表达式模板解决的问题是：

在编译时进行复杂的表达式计算。对于一个数值数组类，它需要为基于整个数组对象的数值操作提供支持

谈到表达式模板，自然联想到前面的template metaprogramming。

表达式模板有时依赖于深层的嵌套模板实例化，而这种实例化又和我们在template metaprogramming中遇到的递归实例化非常相似；
表达式模板、元编程两种实例化技术都是为了支持高性能的数组操作。侧面说明了metaprogramming和表达式模板是息息相关的。当然，这两种技术还是互补的。例如，metaprogramming主要用于小的，大小固定的数组，而表达式模板则适用于能够在运行期确定大小、中等大小的数组。

点乘

向量的点乘可以看作组合体设计模式的一个特例。点乘可以分成两个部分：叶结点是一维向量的积，而组合体是剩下N-1维向量的点乘。

显而易见，这是组合体的某种简并（degenerate）形式，每个组合体包含一个叶结点和一个组合体。使用面向对象编程的技术，我们可以用一个基类和两个派生类来表示点乘：

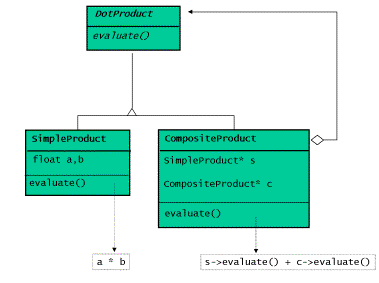
基类:

template <typename T>
class DotProduct
{
   public:
      virtual ~DotProduct () {}
      virtual T eval() = 0;
}

组合体:

template <typename T>
class CompositeDotProduct  : public DotProduct<T>
{
public:
    CompositeDotProduct (T* a, T* b, size_t dim) :
        s(new SimpleDotProduct<T>(a, b)),
        c((dim == 1) ? 0 : new CompositeDotProduct<T>(a + 1, b + 1, dim - 1))
    {}

    virtual ~CompositeDotProduct ()
    {
        delete c;
        delete s;
    }

    virtual T eval()
    {
        return ( s->eval() + ((c) ? c->eval() : 0));
    }

protected:
    SimpleDotProduct<T>* s;
    CompositeDotProduct<T>* c;
};

叶节点：

template <typename T>
class SimpleDotProduct  : public DotProduct<T>
{
public:
   SimpleDotProduct (T* a, T* b) : v1(a), v2(b)
   {}

   virtual T eval()
   {
       return (*v1)*(*v2);
   }
private:
   T* v1;
   T* v2;
};

辅助函数:


template <typename T>
T dot(T* a, T* b, size_t dim)
{
    return (dim == 1) ?
              SimpleDotProduct<T>(a, b).eval() :
              CompositeDotProduct<T>(a, b, dim).eval();
}

调用：

1	int a[4] = {1, 100, 0, -1};
2	int b[4] = {2, 2, 2, 2};
3	std::cout << dot(a, b, 4);

当然，这不是计算点乘的最有效途径。我们可以通过在派生类中消去叶结点和组合体来简化实现。这样，不在构造函数里传递且保存需要计算的向量，以便之后的计算，而是直接将向量传递给求值函数。将构造函数和求值函数由

SimpleDotProduct<T>::SimpleDotProduct (T* a, T* b) : v1(a), v2(b)
{}

virtual T SimpleDotProduct<T>::eval()
{
    return (*v1)*(*v2);
}

修改为一个带参数的求值函数：


T SimpleDotProduct::eval(T* a, T* b, size_t dim)
{
    return (*a)*(*b);
}

现在让我们将面向对象的实现转化成为编译时计算的实现。叶结点和组合体对应的两个类共用了一个用来表示它们的共同操作的基类——这是面向对象编程的常用技巧：共同点用相同的基类来表示。在模板编程中，共同点则是用命名的一致性来表现的。在面向对象编程中的虚函数将不再为虚，而变为一个普通的，有着特定名称的函数。两个派生类不再是从一个基类中派生的两个类，而是变为独立的，有着相同名称和相通记号成员函数的两个类。也就是说，我们不再需要基类了。

现在我们来通过在模板的参数中保存结构信息的方式来实现组合体。我们需要保存的结构信息是这个向量的维度。回忆一下之前我们计算阶乘和平方根的代码：函数实现中函数的参数变为了编译时处理的模板参数。我们在这里也采用相同的手法，原来在面向对象实现中传递给求值函数的向量的维度，在这里变为编译时确定的模板参数。因此在组合体中，这个维度数据将变为模板中的一个常量参数。

叶结点则需要通过组合体类在一维情况下的模板特化类来实现。正如以往一样，我们将运行时的递归转变为编译时的递归：将对求值虚函数的递归调用转变为模板类在递归实例化的过程中对一个静态的求值函数的递归调用。如下是编译时计算点乘代码的类图：

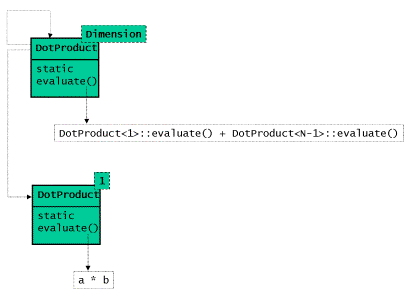
template <size_t N, typename T>
class DotProduct
{
public:
    static T eval(T* a, T* b)
    {
        return  DotProduct<1,T>::eval(a,b) + DotProduct<N-1,T>::eval(a+1,b+1);
    }
};

template <typename T>
class DotProduct<1,T>
{
public:
    static T eval(T* a, T* b)
    {
        return (*a)*(*b);
    }
};

template <size_t N, typename T>
inline T dot(T* a, T* b)
{
    return DotProduct<N,T>::eval(a, b);
}

int a[4] = {1, 100, 0, -1};
int b[4] = {2, 2, 2, 2};
std::cout << dot<4>(a,b);

注意到在运行时计算中，点乘函数的调用方法是dot(a, b, 4)，而编译时计算中，点乘函数的调用方法是dot<4>(a, b)

dot(a, b, 4)等价于CompositeDotProduct<int>().eval(a, b, 4)，递归式的引发如下函数在运行时的调用：

SimpleDotProduct<int>().eval(a, b, 1);
CompositeDotProduct<int>().eval(a + 1, b + 1, 3);
SimpleDotProduct<int>().eval(a + 1, b + 1, 1);
CompositeDotProduct<int>().eval(a + 2, b + 2, 2);
SimpleDotProduct<int>().eval(a + 2, b + 2, 1);
CompositeDotProduct<int>().eval(a + 3, b + 3, 1);
SimpleDotProduct<int>().eval(a + 3, b + 3, 1);

dot<4>(a, b)通过计算DotProduct<4, int>::eval(a, b)，从而递归式的引发下列模板依次实例化展开：

1	DotProduct<4, size_t>::eval(a, b);
2	DotProduct<1, size_t>::eval(a, b) + DotProduct<3, size_t>::eval(a + 1, b + 1);
3	(a) (*b) + DotProduct<1, size_t>::eval(a + 1, b + 1) + DotProduct<2, size_t>::eval(a + 2, b + 2);
4	(a) (b) + (a + 1) * (*b + 1) + DotProduct<1, size_t>::eval(a + 2, b + 2) + DotProduct<1, size_t>::eval(a + 3, b + 3);
5	(a) (b) + (a + 1) * (b + 1) + (a + 2) * (b + 2) + (a + 3) * (*b + 3)

在可执行文件中，只会有(*a) * (*b) + (*a + 1) * (*b + 1) + (*a + 2) * (*b + 2) + (*a + 3) * (*b + 3)对应的代码；具体的展开过程是在编译时完成的。

很明显，模板编程提升了运行时的计算性能，但是代价是延长了编译的时间。递归的模板实例化展开所造成的编译时间延长是以数量级形式进行的。而面向对象的代码虽然编译时间短，却花费了更多的运行时间。

编译时计算的另一个局限性在于，向量的维度必须在编译时就已知，因为这个值需要通过模板参数来传递。实际上这反而不是太大的问题，因为通常这个值在编码的时候的确是已知的，例如，我们如果要计算空间中的向量，那么向量的维度显然是3。

点乘的代码未必能给读者留下深刻印象，因为事实上我们只需要手工展开乘法，就能带来和模板编程带来的相同的性能提升。然而这里所提及的技术并不仅仅局限于点乘，而是可以扩展到高阶矩阵的算术计算上去。这样的编码将大大简化编程的复杂性。如果定义a为 10x20的矩阵，b为20x10的矩阵，而c为10x10的矩阵，那么使用a * b + c来表达计算将显得非常简洁明了。程序员显然宁愿让编译器自动的，同时也是可靠的处理这个问题，而不愿意手工展开如此高阶的矩阵。

算术表达式

形如(a + 1) * c或者log(abs(x - N))的算术表达式将由语法树来实现。共有两种终点表达式：常数（literial）与数值变量（variable）。常数对应的是已知的数值，而数值变量则可能在每次求值时取不同的值。非终点表达式则由一元或者二元运算符组成，每个非终点表达式可能包含一到两个终点表达式。表达式中可能有各种不同语义的运算符，比如+ ，-，*，/，++，–，exp，log，sqrt等等

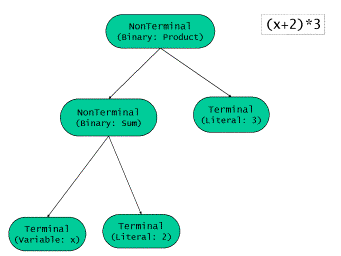
我们通过(x + 2) * 3这个具体实例来分析。组合体的结构，也就是语法树的结构，如下图所示：

设计如下类图所示：

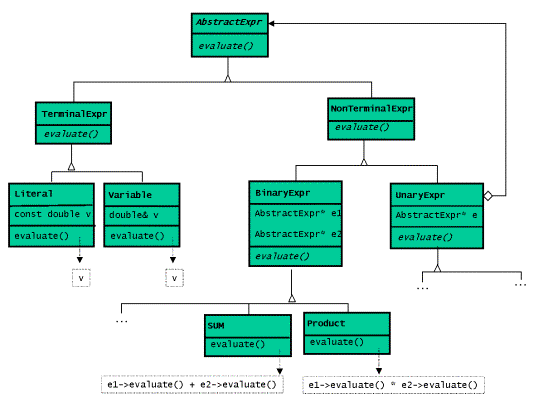
面向对象方式下的算术表达式的解释器

class AbstractExpr
{
public:
    virtual double eval() const = 0; };

class TerminalExpr : public AbstractExpr
{ };

class NonTerminalExpr : public AbstractExpr
{ };

class Literal : public TerminalExpr
{
public:
    Literal(double v) : _val(v)
    {}

    double eval() const
    {
        return _val;
    }

private:
    const double _val;
};

class Variable : public TerminalExpr
{
public:
    Variable(double& v) : _val(v)
    {}

    double eval() const
    {
        return _val;
    }

private:
    double& _val;
};

class BinaryExpr : public NonTerminalExpr
{
protected:
    BinaryExpr(const AbstractExpr* e1, const AbstractExpr* e2) : _expr1(e1),_expr2(e2)
    {}

    virtual ~BinaryExpr ()
    {
        delete const_cast<AbstractExpr*>(_expr1);
        delete const_cast<AbstractExpr*>(_expr2);
    }

    const AbstractExpr* _expr1;
    const AbstractExpr* _expr2; 
};

class Sum : public BinaryExpr
{
public:
    Sum(const AbstractExpr* e1, const AbstractExpr* e2) : BinExpr(e1,e2)
    {}

    double eval() const
    {
        return _expr1->eval() + _expr2->eval();
    }
};

使用解释器来处理算术表达式

void someFunction(double x)
{
    Product expr(new Sum(new Variable(x), new Literal(2)), new Literal(3));
    std::cout << expr.eval() <<std::endl; 
}

首先创造了一个表达式对象，用以表示(x + 2) * 3。之后该对象对自身进行求值。自然而然的，我们觉得这是一个极其低效的计算方法。现在我们将它转化为表达式模板。

正如之前点乘的例子中所示，我们首先要消除所有的虚基类。因为模板类中没有继承，取而代之的是相同的成员名称。因此，我们不再使用基类，而将所有的终点表达式和非终点表达式都用单独的类来表示，它们共有一个相同的名为eval的函数。

下一步，我们将通过类模板UnaryExpr和BinaryExpr来生成所有的形如Sum和Product的非终点表达式。这里结构信息将全部保存在类模板的参数中。这些类模板将其子表达式的类型作为其类型模板。另外，我们将具体的运算符操作抽象为类模板中一个类型，通过仿函数对象传递。

实现，与面向对象实现没有很大的差别。

同样的，运行时递归将由编译时递归所代替：我们将虚的求值函数的递归调用改为表达式模板的递归实例化。

基于模板实现表达式求值问题的类图：

基于模板的算术表达式解释器

class Literal
{
public:
    Literal(const double v) : _val(v)
    {}

    double eval() const
    {
        return _val;
    }

private:
    const double _val;
};

class Variable
{
public:
    Variable(double& v) : _val(v)
    {}

    double eval() const
    {
        return _val;
    }

private:
    double& _val;
};

template <typename ExprT1, typename ExprT2, typename BinOp>
class BinaryExpr
{
public:
    BinaryExpr(ExprT1 e1, ExprT2 e2,BinOp op=BinOp()) :
        _expr1(e1),_expr2(e2),_op(op)
    {}

    double eval() const
    {
        return _op(_expr1.eval(),_expr2.eval());
    }

private:
    ExprT1 _expr1;
    ExprT2 _expr2;
    BinOp  _op;
};

UnaryExpr的类模板与BinaryExpr的类模板相似。对于实际操作，我们可以使用已经编写好的STL的仿函数类plus，minus，等等，或者我们也可以自行编写。一个用来表示和的二元表达式的类型是

1	BinaryExpr<ExprT1, ExprT2, std::plus<double>>

这样的类型使用起来较为复杂，因此我们写一个产生函数，方便以后的使用。

产生函数

产生函数是在模板编程中广泛使用的一种技巧。在STL中有大量的产生函数，例如 make_pair()。产生函数的优势在于，可以利用编译器对函数模板参数的自动推导来简化编程，而对类模板，编译器是无法进行自动推导的。

每次我们从一个类模板中创建一个对象的时候，我们需要给出完整的类模板参数的实例化信息。在很多情况下，这些信息非常复杂，难于理解。例如包含pair的pair：

1	pair<pair<string, complex<double>>
2	pair<string, complex<double>>>

产生函数可以简化这个问题：它将生成给定类型的对象，而无需我们写出冗长的类型声明信息。

更准确的说，产生函数是一类函数模板。这种函数模板与它生成的对象对应的模板类有着相同的模板参数。以pair为例，pair类模板有两个类型参数T1和T2，表示它所包含的两个元素的类型，而make_pair()产生函数同样包含这两个类型参数：

template <typename T1, typename T2>
class pair
{
public:
    pair(T1 t1, T2 t2);
    // ...
};

template <typename T1, typename T2>
pair<T1,T2> make_pair(t1 t1, T2 t2) 
{
    return pair<T1,T2>(t1, t2);
}

产生函数与构造函数非常相似：我们传递给产生函数的参数和我们传递给构造函数的参数是一样的。因为编译器能够自动推导函数模板中模板参数所表示的类型，我们可以借此省去这个声明，而把这一繁重的工作交给编译器来进行。因此，我们不用通过

1	pair< pair<string,complex<double>>, pair<string,complex<double>>>(
2	pair<string,complex<double> >("origin", complex<double>(0,0)),
3	pair<string,complex<double> >("saddle", aCalculation()))

来声明一个复杂的pair，而通过产生函数进行：

1	make_pair(make_pair("origin", complex<double>(0,0)), make_pair("saddle", aCalculation()))

我们将用产生函数来简化表达式对象的生成。列表12给出了产生函数的两个例子：

template  <typename ExprT1, typename ExprT2>
BinaryExpr<ExprT1,ExprT2,plus<double>> makeSum(ExprT1 e1, ExprT2 e2)
{
    return BinaryExpr<ExprT1,ExprT2,plus<double> >(e1,e2);
}

template  <typename ExprT1, typename ExprT2>
BinaryExpr <ExprT1,ExprT2,multiplies<double>> makeProd(ExprT1 e1, ExprT2 e2)
{
    return BinaryExpr<ExprT1,ExprT2,multiplies<double> >(e1,e2);
}

基于模板实现的解释器解析(x + 2) * 3的方式：


void someFunction (double x)
{
    BinaryExpr< BinaryExpr < Variable, Literal, plus<double> >, multiplies<double>>
            expr = makeProd (makeSum (Variable(x), Literal(2)), Literal(3));
    cout << expr.eval() << endl; 
}

首先生成了一个代表(x + 2) * 3的表达式对象，然后这个对象对自身进行求值。表达式对象的结构本身即是语法树的结构。
我们其实完全不必给出如此冗长的类型信息，而是可以直接使用产生函数来自动生成

1	std::cout << makeProd(makeSum(Variable(x),Literal(2)),Literal(3)).eval() << std::endl;

通过模板来实现解释器这个设计模式的优越性是什么呢？

倘若所有的产生函数，构造函数和求值函数都能被编译器内联的话（这应该是可以办到的，因为这些函数本身都很简单），表达式makeProd(makeSum(Variable(x),Literal(2)),Literal(3)).eval()最终将被编译器转化为(x + 2) * 3进行编译。

回过头来看前面的代码

1	Product expr(new Sum(new Variable(x),new Literal(2)), new Literal(3)).eval()

仅仅这一小段中就包含了大量的堆上的内存申请和对象构造，同时也引入了不少对虚函数eval()的调用。这些虚函数调用很难被内联，因为编译器一般不会内联通过指针调用的函数。

基于模板的实现将比面向对象的实现效率高上许多。

为了使用上的方便，我们进一步的修改表达式模板。首先要考虑的是增加可读性。

将产生函数修改为重载的运算符。也就是说，将makeSum改为operator+，将 makeProd改为operator*，等等。这样产生的效果就是将

1	//from
2	makeProd(makeSum(Variable(x), Literal(2)), Literal(3))
3	//to
4	((Variable(x) + Literal(2)) * Literal(3))

这已经是一大进步了。但是距离我们所希望的直接写(x + 2) * 3还有一定差距。因此我们需要设法消除Variable和Literal的构造函数的直接调用。

将产生函数从makeSum改为operator+

template <typename ExprT1, typename ExprT2>
BinaryExpr<ExprT1, ExprT2, plus<double>> operator+(ExprT1 e1, ExprT2 e2)
{
		return BinaryExpr<ExprT1, ExprT2, plus<double>>(e1,e2);
}

我们希望x + 2可以和之前的makeSum(x, 2)，如今的operator+(x, 2)相对应。x + 2应当创造一个代表求和的二元表达式对象，而这个对象的构造函数将以double类型的变量x以及整形常量2作为构造参数。

更准确的说，这将生成一个BinaryExpr<double, int, plus<double>>(x, 2)的匿名对象。然而我们所期望的类型并非如此：需要的是BinaryExpr <Variable, Literal, plus<double>>类型的对象。可是，自动模板参数类型推导并不知道x是一个变量，而2是一个常量。编译器只能检查传递给函数的参数类型，从而从x中推导出double类型，从2中推导出int类型。

看起来我们需要稍稍给编译器一些更多的信息，从而得到我们所需要的结果。如果我们给函数传递的不是double类型的x，而是一个Variable类型的参数，那么编译器应该能够自动产生BinaryExpr<Variable, int, plus<double>>，这将更接近我们的目标。（我们将很快解决int到Literal的转换问题）因此，用户不得不对代码做一些小小的改动：他们需要用Variable类来包装他们的变量。

void someFunction (double x)
{
    Variable v = x;
    cout << ((v + 2) * 3).eval() << endl; 
}

通过使用Variable对象v来代替一个数值类型的参数，我们可以将v + 2转化为一个等价于BinaryExpr<Variable, int, plus<double>>(v, 2)的匿名对象。这样的BinaryExpr对象有两个数据成员，一个是Variable，一个是int。

求值函数BinaryExpr<Variable, int, plus<double>>::eval()将计算并且返回两个数据成员的和。问题是，int类型的数据无法自行转化为可以自动求值的对象，我们必须将常数2转化为Literal类型，才能进行自动求值。如何做到这种自动转化呢？我们需要使用traits。

Traits TRAITS
在模板编程中，traits是另一种常用的技术。traits类是一种只与另外一种类型配合，保存这种类型的具体信息的影子类（shadow class）。

C++ STL中有多个traits的例子，字符traits就是其中之一。读者大约知道标准库中的string类其实是一个类模板，这个类模板的参数是具体的字符类型。这就使得string可以处理普通的字符和宽字符。实际上，string类的实际名称是basic_string。basic_string可以通过实例化来接受任何类型的字符，而不仅仅是上述提及的两种。倘若有人需要保存以Jchar定义的日文字符，那么他就可以用basic_string模板实现：basic_string。

读者可以自己设想如何设计这样的string类模板。有一些必须的信息并不能由字符的类型本身所提供。例如，如何计算字符串的长度？这可以通过数一下字符串里的所有字符个数来实现。这样就需要知道字符串的结束记号是什么。但是如何知道这一点呢？虽然我们知道对于一般的字符，’\0’是结束符；宽字符wchar_t有它自己定义的结束符，但是对于Jchar呢？很明显，结束符这个信息与字符的类型直接相关，但是却不包括在类型本身所能提供的信息之中。这时traits就派上了用场：它们可以提供这些额外的，却是必须的信息。

traits类型是一种可以被具体的一组类型实例化或者特化的影子（shadow）类模板，在实例化或者特化的时候，它们包含了额外的信息。C++标准库中字符的traits，即是char_traits类模板，就包含了一个静态的字符常量，用以表示这种字符对应的字符串结束符的值。

我们使用traits技术来解决常数到Literal类型的转换问题。对于每一种表达式的类型，我们定义表达式的traits用以保存它们在各种运算符对象中的存储方式。所有的常数类型都应该以Literal类型的对象保存；所有的Variable对象都应该以本身的类型保存在Variables之中；而所有的非终端表达式都应该按照本身类型保存。

表达式traits

template <typename ExprT>
struct exprTraits
{
    typedef ExprT expr_type;
};

template <>
struct exprTraits<double>
{
    typedef Literal expr_type;
};

template <>
struct exprTraits<int>
{
    typedef Literal expr_type;
};

表达式traits类定义了一个嵌套类型expr_type，代表表达式对象的具体类型。未特化的traits模板类将所有常用的表达式类型保存为其本身。但是对于C++语言内置的数值类型，例如short，int，long，float，double等则进行了特化，它们在表达式中对应的类型均为Literal。

在BinaryExpr和UnaryExpr类中，我们将使用表达式traits来确认存有子表达式的数据成员的类型。

使用表达式traits

template <typename ExprT1, typename ExprT2, typename BinOp>
class BinaryExpr
{
public:
    BinaryExpr(ExprT1 e1, ExprT2 e2,BinOp op=BinOp()) :
        _expr1(e1), _expr2(e2), _op(op)
    {}

    double eval() const
    {
        return _op(_expr1.eval(),_expr2.eval());
    }

private:
    exprTraits<ExprT1>::expr_type _expr1;
    exprTraits<ExprT2>::expr_type _expr2;
    BinOp  _op;
};

通过使用表达式traits，BinaryExpr<Variable, int, plus<double>>可以将它的两个运算元的类型分别保存为Variable和Literal。

现在我们已经可以使用((v + 2) * 3).eval()来进行求值了。在这里v是一个Variable类型，其中封装了一个double类型的对象x。这样，实际上的求值就是(x + 2) * 3了。我们可以为可读性着想，稍稍再做进一步的改进。人们通常觉得调用表达式的一个成员函数进行求值看上去很古怪。不过我们可以设计一个辅助函数，将((v + 2) * 3).eval()变为eval((v + 2) * 3)。这两段代码虽然事实上是等价的，但是却更符合诸君的阅读习惯。

1	template <class ExprT> double eval(ExprT e)
2	{
3	return e.eval();
4	}

下图给出了表达式((v + 2) * 3).eval()在v作为Variable封装了一个double类型的x的情况下，在编译过程中是如何逐步的展开为(x + 2) * 3的。

表达式对象的反复计算:

我们所用到的语法树都是静态的。每个语法树在构造之后，只被调用一次。然而我们可以通过给定一个语法树，并传入不同的参数值，来动态的使用这个模型。如上文所述，我们希望能够用如下的近似函数：

template <class ExprT>
double integrate (ExprT e,double from,double to,size_t n)
{
    double sum = 0;
    double step = (to - from) / n;
    for (double i = from + step / 2; i < to; i += step)
        sum += e.eval(i);
    return step * sum;
}

计算类似下面的积分式：

1	\int_{1.0}^{5.0}
2	\frac{x}{1 + x}
3	\,dx

1	Identity<double> x;
2	cout << integrate(x / (1.0 + x), 1.0, 5.0, 10) << endl;

这里我们需要的是一个被反复调用的表达式对象，然而我们现有的代码尚不支持这样的操作。不过一些小小的修改即可满足我们的要求。只要让我们的eval函数接受一个值作为参数即可。非终端的表达式将把参数传递给它们的子表达式。Literal类只需要形式上的接受这个参数即可，它们的值不受这个参数所影响。Variable将不再返回Variable的值，而是它所接受到的这个参数的值。出于这个目的，我们把Variable改名为Identity。

class Literal
{
public:
    Literal(double v) : _val(v)
    {}

    double eval(double) const
    {
        return _val;
    }

private:
    const double _val;
};

template<class T> class Identity
{
public:
    T eval(T d) const
    {
        return d;
    }
};

template <class ExprT1,class ExprT2, class BinOp> class BinExpr
{
public:
    double eval(double d) const
    {
        return _op(_expr1.eval(d),_expr2.eval(d));
    }
};

如果编写sqrt()，sqr()，exp()，log()等等数值函数的非终点表达式代码，甚至可以计算高斯分布：

double sigma = 2.0;
double mean = 5.0;
const double Pi = 3.141593;
cout << integrate(
        1.0 / (sqrt(2 * Pi) * sigma) * exp(sqr(x - mean) / (-2 * sigma * sigma)),
        2.0, 10.0, 100) << endl;

我们可以通过调用C标准库里的相应函数来实现这些非终点表达式，只要增加相应的一元或者二元运算符的产生函数即可。

template  <typename ExprT>
UnaryExpr<ExprT, double(*)(double)> sqrt(const ExprT& e)
{
    return UnaryExpr<ExprT, double(*)(double)>(e, ::std::sqrt);
}

template  <typename ExprT>
UnaryExpr<ExprT, double(*)(double)> exp(const ExprT& e)
{
    return UnaryExpr<ExprT,double(*)(double)>(e,::std::exp);
}

通过这些修改，我们得到了一个有力的高性能数值表达式计算库。利用前述所述的技术，不难为这个库增添逻辑计算的功能。如果将求值函数eval()改为括号算符的重载operator()()，我们可以很容易的将表达式对象转换为仿函数对象，这样就可以应用在STL的算法库中。下面是一个将逻辑表达式应用于计算链表中符合条件的元素个数的例子：

1	list<int> l;
2	Identity<int> x;
3	count_if(l.begin(), l.end(), x >= 10 && x <= 100);

一旦编写好相应的表达式模板，就可以如上述例子所示一般，令代码兼具高度可读性和高效的运行时表现。建立这样的表达式模板库则相当复杂，需要使用本文尚未提及的许多模板编程技巧。但是无论如何，本文中涉及的编程原理已经覆盖了所有的模板库。

类型区分

开发某些相对较小、并且互相独立的功能，而且对于这些简单功能而言，模板是最好的实现方法：

一个用于类型区分的框架；
智能指针
tuple
仿函数

辨别基本类型

主要介绍用模板实现对类型的辨识，判断其是内建类型、指针类型、class类型或者其他类型中的哪一种。

缺省情况下，我们一方面假定一个类型不是一个基本类型，另一方面我们为所有的基本类型都特化给模板：

// 基本模板：一般情况下T不是基本类型
template <typename T>
class IsFundaT
{
    public:
        enum { Yes = 0, No = 1 };
};

// 用于特化基本类型的宏
#define MK_FUNDA_TYPE(T)                 \
template<> class IsFundaT<T> {            \
    public:                                                \
        enum { Yes = 1, No = 0 };                \
};

MK_FUNDA_TYPE(void)

MK_FUNDA_TYPE(bool)
MK_FUNDA_TYPE(char)
MK_FUNDA_TYPE(signed char)
MK_FUNDA_TYPE(unsigned char)
MK_FUNDA_TYPE(wchar_t)

MK_FUNDA_TYPE(signed short)
MK_FUNDA_TYPE(unsigned short)
MK_FUNDA_TYPE(signed int)
MK_FUNDA_TYPE(unsigned int)
MK_FUNDA_TYPE(signed long)
MK_FUNDA_TYPE(unsigned long)

#if LONGLONG_EXISTS
MK_FUNDA_TYPE(signed long long)
MK_FUNDA_TYPE(unsigned long long)
#endif   // LONGLONG_EXISTS

MK_FUNDA_TYPE(float)
MK_FUNDA_TYPE(double)
MK_FUNDA_TYPE(long double)

辨别组合类型

组合类型是指一些构造自其他类型的类型。简单的组合类型包括：

普通类型
指针类型
引用类型
数组类型

它们都是构造自单一的基本类型。同时，class类型和函数类型也是组合类型，但这些组合类型通常都会涉及到多种类型（例如参数或者成员的类型）。在此，我们先考虑简单的组合类型；

另外，我们还将使用局部特化对简单的组合类型进行区分。接下来，我们将定义一个trait类，用于描述简单的组合类型；而class类型和枚举类型将在最后考虑。

template <typename T>
class CompoundT                // 基本模板
{
    public:
        enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0, IsFuncT = 0, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef T BottomT;
        typedef CompoundT<void> ClassT;
};

成员类型BaseT指的是：用于构造模板参数类型T的（直接）类型；而BottomT指的是最终去除指针、引用和数组之后的、用于构造T的原始类型。例如，如果T是int**,那么BaseT将是int*，而BottomT将会是int类型。对于成员指针类型，BaseT将会是成员的类型，而ClassT将会是成员所属的类的类型。例如，如果T是一个类型为int(X:😗)()的成员函数指针，那么BaseT将会是函数类型int()，而ClassT的类型则为X。如果T不是成员指针类型，那么ClassT将会是CompoundT（这个选择并不是必须的，也可以使用一个noclass来作为ClassT）。

其中，针对指针和引用的局部特化是相当直接的：

template <typename T>
class CompoundT<T&>
{
    public:
        enum { IsPtrT = 0, IsRefT = 1, IsArrayT = 0,
                    IsFuncT = 0, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef typename CompoundT<T>::BottomT BottomT;
        typedef CompoundT<void> ClassT;
};

template <typename T>
class CompoundT<T*>
{
    public:
        enum { IsPtrT = 1, IsRefT = 0, IsArrayT = 0,
                    IsFuncT = 0, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef typename CompoundT<T>::BottomT BottomT;
        typedef CompoundT<void> ClassT;
};

对于成员指针和数组，我们可能会使用同样的技术来处理。但是，在下面的代码中我们将发现，与基本模板相比，这些局部特化将会涉及到更多的模板参数：


template<typename T, size_t N>
class CompoundT<T[N]>
{
    public:
        enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 1,
                    IsFuncT = 0, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef typename CompoundT<T>::BottomT BottomT;
        typedef CompoundT<void> ClassT;
};

template<typename T>
class CompoundT<T[]>
{
    public:
        enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 1,
                    IsFuncT = 0, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef typename CompoundT<T>::BottomT BottomT;
        typedef CompoundT<void> ClassT;
};

template<typename T>
class CompoundT<T C::*>
{
    public:
        enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
                    IsFuncT = 0, IsPtrMemT = 1 };
        typedef T BaseT;
        typedef typename CompoundT<T>::BottomT BottomT;
        typedef C ClassT;
};

辨别函数类型

使用SFINAE原则的解决方案：

一个重载函数模板的后面可以是一些显式模板实参；而且对于某些重载函数类型而言，该实参是有效的，但对于其他的重载函数类型，该实参则可能是无效的。实际上，后面使用重载解析对枚举类型进行辨别的技术也使用到了这种方法。

SFINAE原则在这里的主要用处是：

找到一种构造，该构造对函数类型是无效的，但是对于其他类型都是有效的；或者完全相反。由于前面我们已经能够辨别出几种类型了，所以我们在此可以不再考虑这些（已经可以辨别的）类型。
因此，针对上面这种要求，数组类型就是一种有效的构造；因为数组的元素是不能为void值、引用或者函数的。故而可以编写如下代码

template <typename T>
class IsFunctionT
{
    private:
        typedef char One;
        typedef struct { char a[2]; } Two;
        template <typename U> static One test ( ... );
        template <typename U> static Two test ( U (*)[1] );
		// 不理解，下面的IsFunctionT<T>::test<T>(0)怎么匹配？
    public:
        enum { Yes = sizeof(IsFunctionT<T>::test<T>(0)) == 1 };
        enum { No = !Yes };
};

借助于上面这个模板定义，只有对于那些不能作为数组元素类型的类型，IsFunctionT::Yes才是非零值（即为1）。另外，我们应该知道该方法也有一个不足之处；并非只有函数类型不能作为数组元素类型，引用类型和void类型同样也不能作为数组元素类型。
幸运的是，我们可以通过为引用类型提供局部特化，以及为void类型提供显式特化，来解决这个不足：

template <typename T>
class IsFunctionT<T&>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

template <>
class IsFunctionT<void>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

template <>
class IsFunctionT<void const>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

至此，我们可以重新改写基本的CompoundT模板如下：

template <typename T>
class IsFunctionT
{
    private:
        typedef char One;
        typedef struct { char a[2]; } Two;
        template <typename U> static One test ( ... );
        template <typename U> static Two test ( U (*)[1] );
    public:
        enum { Yes = sizeof(IsFunctionT<T>::test<T>(0)) == 1 };
        enum { No = !Yes };
};

template <typename T>
class IsFunctionT<T&>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

template <>
class IsFunctionT<void>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

template <>
class IsFunctionT<void const>
{
    public:
        enum { Yes = 0 };
        enum { No = !Yes };
};

// 对于void volatile 和 void const volatile类型也是一样的
...

template <typename T>
class CompoundT                // 基本模板
{
    public:
        enum { IsPtrT = 0, IsRefT = 0, IsArrayT = 0,
                    IsFuncT = IsFunctionT<T>::Yes, IsPtrMemT = 0 };
        typedef T BaseT;
        typedef T BottomT;
        typedef CompoundT<void> ClassT;
};

运用重载解析辨别枚举类型

重载解析是一个过程，它会根据函数参数的类型，在多个同名函数中选择出一个合适的函数。
接下来我们将看到，即使没有进行实际的函数调用，我们也能够利用重载解析来确定所需要的结果。

总之，对于测试某个特殊的隐式转型是否存在的情况，利用重载解析的方法是相当有用的。
在此，我们将要利用从枚举类型到整型的隐式转型：它能够帮助我们分辨枚举类型。

struct SizeOverOne { char c[2]; };

template<typename T,
                bool convert_possible = !CompoundT<T>::IsFuncT &&
                                                   !CompoundT<T>::IsArrayT>
class ConsumeUDC
{
    public:
        //在ConsumeUDC模板中已经强制定义了一个到T的自定义转型
        operator T() const;
};

// 到函数类型的转型是不允许的
// 如果由基本模板得到的convert_possible为false,则匹配此特化；不转型-->无自定义转型操作
template<typename T>
class ConsumeUDC<T, false>
{
};

// 到void类型的转型是不允许的
template <bool convert_possible>
class ConsumeUDC<void, convert_possible>
{
};

char enum_check(bool);
char enum_check(char);
char enum_check(signed char);
char enum_check(unsigned char);
char enum_check(wchar_t);

char enum_check(signed short);
char enum_check(unsigned short);
char enum_check(signed int);
char enum_check(unsigned int);
char enum_check(signed long);
char enum_check(unsigned long);

#if LONGLONG_EXISTS
    char enum_check(signed long long);
    char enum_check(unsigned long long);
#endif     // LONGLONG_EXISTS

// 避免从float到int的意外转型
char enum_check(float);
char enum_check(double);
char enum_check(long double);

SizeOverOne enum_check( ... );         // 捕获剩余所有情况
template<typename T>
class IsEnumT
{
    public:
        enum {
            Yes = IsFundaT<T>::No &&
                    !CompoundT<T>::IsRefT &&
                    !CompoundT<T>::IsPtrT &&
                    !CompoundT<T>::IsPtrMemT &&
                    sizeof(enum_check(ConsumeUDC<T>())) == 1
                }
        enum { No = !Yes };
};

上面代码的核心在于后面的一个sizeof表达式，它的参数是一个函数调用。也就是说，该sizeof表达式将会返回函数调用返回值的类型的大小；其中，将应用重载解析原则来处理enum_check()调用；但另一方面，我们并不需要函数定义，因为实际上并没有真正调用该函数。在上面的例子中，如果实参可以转型为一个整型，那么enum_check()将返回一个char值，其大小为1。对于其他的所有类型，我们使用了一个省略号函数（即enum_check( … ) ），然而，根据重载解析原则的优先顺序，省略号函数将会是最后的选择。在此，我们对enum_check()的省略号版本进行了特殊的处理，让它返回一个大小大于一个字节的类型（即SizeOverOne）。

对于函数enum_check的调用实参，我们必须仔细地考虑。首先，我们并不知道T是如何构造的，或许将会调用一个特殊的构造函数。为了解决这个问题，我们可以声明一个返回类型为T的函数，然后通过调用这个函数来创建一个T。由于处于sizeof表达式内部，因此该函数实际上并不需要具有函数定义。事实上，更加巧妙的是：对于一个class类型T，重载解析是有可能选择一个针对整型的enum_check()声明的，但前提是该class必须定义一个到整型的自定义转型（有时也称为UDC）函数。到此，问题已经解决了。因为我们在ConsumeUDC模板中已经强制定义了一个到T的自定义转型，该转型运算符同时也为sizeof运算符生成了一个类型为T的实参。下面我们详细分析下：

最开始的实参是一个临时的ConsumeUDC对象；
如果T是一个基本整型，那么将会借助于（ConsumeUDC的）转型运算符来创建一个enum_check()的匹配，该enum_check()以T为实参；
如果T是一个枚举类型，那么将会借助于（ConsumeUDC的）转型运算符，先把类型转化为T，然后调用（从枚举类型到整型的）类型提升，从而能够匹配一个接收转型参数的enum_check()函数（通常而言是enum_check(int)）；
如果T是一个class类型，而且已经为该class自定义了一个到整型的转型运算符，那么这个转型运算符将不会被考虑。因为对于以匹配为目的的自定义转型而言，最多只能调用一次；而且在前面已经使用了一个从ConsumeUDC到T的自定义转型，所以也就不允许再次调用自定义转型。也就是说，对enum_check()函数而言，class类型最终还是未能转型为整型。
如果最终还是不能让类型T于整型互相匹配，那么将会选择enum_check()函数的省略号版本。

最后，由于我们这里只是为了辨别枚举类型，而不是基本类型或者指针类型，所有我们使用了前面已经开放的IsFundaT和CompoundT类型，从而能够排除这些令IsEnumT::Yes成为非零的其他类型，最后使得只有枚举类型的IsEnumT::Yes才等于1。

辨别class类型

使用排除原理：如果一个类型不是一个基本类型，也不是枚举类型和组合类型，那么该类型就只能是class类型。

template <typename T>
class IsClassT
{
    public:
        enum {
            Yes = IsFundaT<T>::No &&
                    IsEnumT<T>::No &&
                    !CompoundT<T>::IsPtrT &&
                    !CompoundT<T>::IsRefT &&
                    !CompoundT<T>::IsArrayT &&
                    !CompoundT<T>::IsPtrMemT &&
                    !CompoundT<T>::IsFuncT
                };
        enum { No = !Yes };
};

模板元编程与可变模板编程

模版元基本概念

模版元程序由元数据和元函数组成，元数据就是元编程可以操作的数据，即C++编译器在编译期可以操作的数据。
元数据不是运行期变量，只能是编译期常量，不能修改，常见的元数据有

enum枚举常量
静态常量
基本类型
自定义类型

元函数是模板元编程中用于操作处理元数据的“构件”，可以在编译期被“调用”，因为它的功能和形式和运行时的函数类似，而被称为元函数，它是元编程中最重要的构件。元函数实际上表现为C++的一个类、模板类或模板函数，它的通常形式如下：

template<int N, int M>
struct meta_func
{
    static const int value = N+M;
}

调用元函数获取value值：cout<<meta_func<1, 2>::value<<endl;
meta_func的执行过程是在编译期完成的，实际执行程序时，是没有计算动作而是直接使用编译期的计算结果的。元函数只处理元数据，元数据是编译期常量和类型，所以下面的代码是编译不过的：

1	int i = 1, j = 2;
2	meta_func<i, j>::value; //错误，元函数无法处理运行时普通数据

模板元编程产生的源程序是在编译期执行的程序，因此它首先要遵循C和模板的语法，但是它操作的对象不是运行时普通的变量，因此不能使用运行时的C关键字（如if、else、for），可用的语法元素相当有限，最常用的是：

enum、static const，用来定义编译期的整数常量；

typedef/using，用于定义元数据；
T、Args…，声明元数据类型；
template，主要用于定义元函数；
“::”，域运算符，用于解析类型作用域获取计算结果（元数据）

如果模板元编程中需要if-else、for等逻辑时该怎么办呢？

模板元中的if-else可以通过type_traits来实现。
type_traits不仅仅可以在编译期做判断，还可以做计算、查询、转换和选择。

模板元中的for等逻辑可以通过递归、重载、和模板特化（偏特化）等方法实现。

type_traits

type_traits是C++11提供的模板元基础库，通过type_traits可以实现在编译期计算、查询、判断、转换和选择，提供了模板元编程需要的一些常用元函数。下面来看看一些基本的type_traits的基本用法。

最简单的一个type_traits是定义编译期常量的元函数integral_constant，它的定义如下：

1	template< class T, T v >
2	struct integral_constant;

借助这个简单的trait，我们可以很方便地定义编译期常量，比如定义一个值为1的int常量可以这样定义：

1	using one_type = std::integral_constant<int, 1>;

或者

1	template<class T>
2	struct one_type : std::integral_constant<int, 1>{};

获取常量则通过one_type::value来获取，这种定义编译期常量的方式相比C98/03要简单，在C98/03中定义编译期常量一般是这样定义的：

template<class T>
struct one_type
{
    enum{value = 1};
};

template<class T>
struct one_type
{
    static const int value = 1;
};

可以看到，通过C11的type_traits提供的一个简单的integral_constant就可以很方便的定义编译期常量，而无需再去通过定义enum和static const变量方式去定义编译期常量了，这也为定义编译期常量提供了另外一种方法。C11的type_traits已经提供了编译期的true和false，是通过integral_constant来定义的：

1	typedef integral_constant<bool, true> true_type;
2	typedef integral_constant<bool, false> false_type;

除了这些基本的元函数之外，type_traits还提供了丰富的元函数，比如用于编译期判断的元函数：

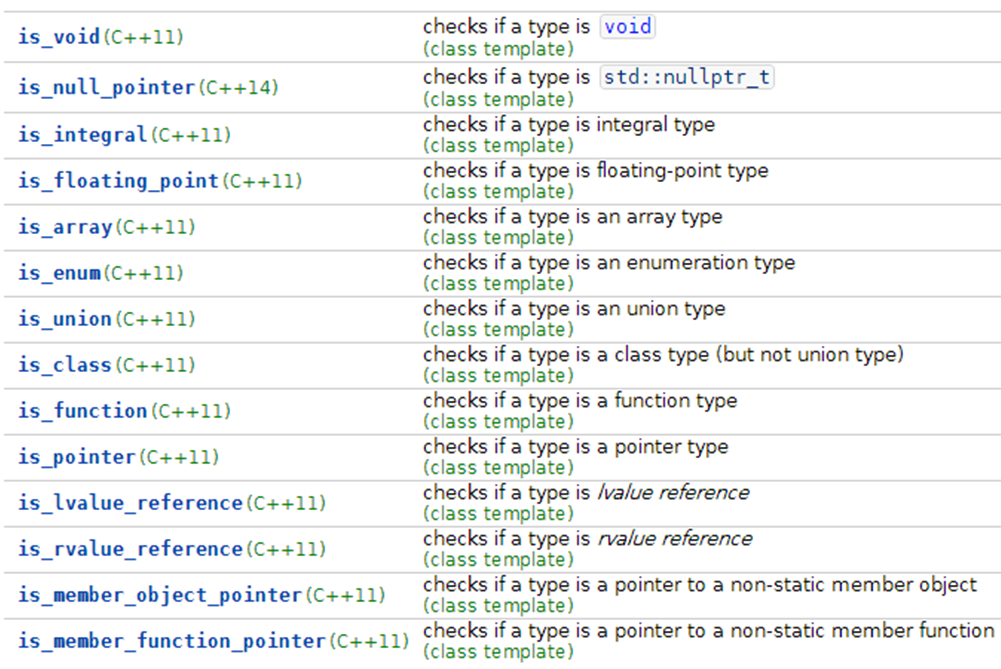
这只是列举一小部分的type_traits元函数，c++11 type_traits提供了上百个方便的元函数
这些基本的元函数用法比较简单：

#include <iostream>
#include <type_traits>

int main() {
  std::cout << "int: " << std::is_const<int>::value << std::endl;
  std::cout << "const int: " << std::is_const<const int>::value << std::endl;

  //判断类型是否相同
  std::cout<< std::is_same<int, int>::value<<"\n";// true
  std::cout<< std::is_same<int, unsignedint>::value<<"\n";// false

  //添加、移除const
  cout << std::is_same<const int, add_const<int>::type>::value << endl;
  cout << std::is_same<int, remove_const<const int>::type>::value << endl;

  //添加引用
  cout << std::is_same<int&, add_lvalue_reference<int>::type>::value << endl;
  cout << std::is_same<int&&, add_rvalue_reference<int>::type>::value << endl;

  //取公共类型
  typedef std::common_type<unsigned char, short, int>::type NumericType;
  cout << std::is_same<int, NumericType>::value << endl;

  return 0;
}

type_traits还提供了编译期选择traits：std::conditional，它在编译期根据一个判断式选择两个类型中的一个，和条件表达式的语义类似，类似于一个三元表达式。它的原型是：

1	template< bool B, class T, class F >
2	struct conditional;

用法很简单：

#include <iostream>
#include <type_traits>

int main()
{
    typedef std::conditional<true,int,float>::type A;               // int
    typedef std::conditional<false,int,float>::type B;              // float

    typedef std::conditional<(sizeof(long long) >sizeof(long double)),
    long long, long double>::type max_size_t;

    cout<<typeid(max_size_t).name()<<endl;  //long double
}

另外一个常用的type_traits是std::decay(朽化)，它对于普通类型来说std::decay（朽化）是移除引用和cv符，大大简化了我们的书写。除了普通类型之外，std::decay还可以用于数组和函数，具体的转换规则是这样的：

先移除T类型的引用，得到类型U，U定义为remove_reference::type。

如果is_array::value为 true，修改类型type为remove_extent::type *。
否则，如果is_function::value为 true，修改类型type将为add_pointer::type。
否则，修改类型type为 remove_cv::type。

std::decay的基本用法：

typedef std::decay<int>::type A;           // int
typedef std::decay<int&>::type B;          // int
typedef std::decay<int&&>::type C;         // int
typedef std::decay<constint&>::type D;    // int
typedef std::decay<int[2]>::type E;        // int*
typedef std::decay<int(int)>::type F;      // int(*)(int)

std::decay除了移除普通类型的cv符的作用之外，还可以将函数类型转换为函数指针类型，从而将函数指针变量保存起来，以便在后面延迟执行，比如下面的例子。

template<typename F>
struct SimpFunction
{
    using FnType = typename std::decay<F>::type;//先移除引用再添加指针

    SimpFunction(F& f) : m_fn(f){}

    void Run()
    {
        m_fn();
    }

    FnType m_fn;
};

如果要保存输入的函数，则先要获取函数对应的函数指针类型，这时就可以用std::decay来获取函数指针类型了，using FnType = typename std::decay<F>::type;实现函数指针类型的定义。type_traits还提供了获取可调用对象返回类型的元函数：std::result_of，它的基本用法：

int fn(int) {return int();}                            // function
typedef int(&fn_ref)(int);                             // function reference
typedef int(*fn_ptr)(int);                             // function pointer
struct fn_class { int operator()(int i){return i;} };  // function-like class

int main() {
  typedef std::result_of<decltype(fn)&(int)>::type A;  // int
  typedef std::result_of<fn_ref(int)>::type B;         // int
  typedef std::result_of<fn_ptr(int)>::type C;         // int
  typedef std::result_of<fn_class(int)>::type D;       // int
}

type_traits还提供了一个很有用的元函数std::enable_if，它利用SFINAE(substitude failure is not an error)特性，根据条件选择重载函数的元函数std::enable_if，它的原型是：

1	template<bool B, class T = void> struct enable_if;

根据enable_if的字面意思就可以知道，它使得函数在判断条件B仅仅为true时才有效，它的基本用法：

template <class T>
typename std::enable_if<std::is_arithmetic<T>::value, T>::type foo(T t)
{
    return t;
}
auto r = foo(1); //返回整数1
auto r1 = foo(1.2); //返回浮点数1.2
auto r2 = foo(“test”); //compile error

在上面的例子中对模板参数T做了限定，即只能是arithmetic（整型和浮点型）类型，如果为非arithmetic类型，则编译不通过，因为std::enable_if只对满足判断式条件的函数有效，对其他函数无效。

可以通过enable_if来实现编译期的if-else逻辑，比如下面的例子通过enable_if和条件判断式来将入参分为两大类，从而满足所有的入参类型：

template <class T>
typename std::enable_if<std::is_arithmetic<T>::value, int>::type foo1(T t)
{
    cout << t << endl;
    return 0;
}

template <class T>
typename std::enable_if<!std::is_arithmetic<T>::value, int>::type foo1(T &t)
{
    cout << typeid(T).name() << endl;
    return 1;
}

对于arithmetic类型的入参则返回0，对于非arithmetic的类型则返回1，通过arithmetic将所有的入参类型分成了两大类进行处理。从上面的例子还可以看到，std::enable_if可以实现强大的重载机制，因为通常必须是参数不同才能重载，如果只有返回值不同是不能重载的，而在上面的例子中，返回类型相同的函数都可以重载。

C11的type_traits提供了近百个在编译期计算、查询、判断、转换和选择的元函数，为我们编写元程序提供了很大的便利。如果说C11的type_traits让模版元编程变得简单，那么C++11提供的可变模板参数和tuple则进一步增强了模板元编程。

可变模板参数

概述

C11的新特性–可变模版参数（variadic templates）是C11新增的最强大的特性之一，它对参数进行了高度泛化，它能表示0到任意个数、任意类型的参数。相比C++98/03，类模版和函数模版中只能含固定数量的模版参数，可变模版参数无疑是一个巨大的改进。

然而由于可变模版参数比较抽象，使用起来需要一定的技巧，所以它也是C11中最难理解和掌握的特性之一。虽然掌握可变模版参数有一定难度，但是它却是C11中最有意思的一个特性。

可变模版参数的展开

可变参数模板和普通模板的语义是一样的，只是写法上稍有区别，声明可变参数模板时需要在typename或class后面带上省略号“…”。比如我们常常这样声明一个可变模版参数：template<typename…>或者template<class…>，一个典型的可变模版参数的定义是这样的：

1	template <class... T>
2	void f(T... args);

可变模版参数的定义当中，省略号的作用有两个：

声明一个参数包T… args，这个参数包中可以包含0到任意个模板参数；
在模板定义的右边，可以将参数包展开成一个一个独立的参数。

参数args前面有省略号，所以它就是一个可变模版参数，我们把带省略号的参数称为“参数包”，它里面包含了0到N（N>=0）个模版参数。我们无法直接获取参数包args中的每个参数的，只能通过展开参数包的方式来获取参数包中的每个参数，这是使用可变模版参数的一个主要特点，也是最大的难点，即如何展开可变模版参数。

可变模版参数和普通的模版参数语义是一致的，所以可以应用于函数和类，即可变模版参数函数和可变模版参数类，然而，模版函数不支持偏特化，所以可变模版参数函数和可变模版参数类展开可变模版参数的方法还不尽相同，下面我们来分别看看他们展开可变模版参数的方法

可变模版参数函数

一个简单的可变模版参数函数：

1	template <class... T>
2	void f(T... args)
3	{
4	cout << sizeof...(args) << endl; //打印变参的个数
5	}
6
7	f(); //0
8	f(1, 2); //2
9	f(1, 2.5, ""); //3

f()没有传入参数，所以参数包为空，输出的size为0，后面两次调用分别传入两个和三个参数，故输出的size分别为2和3。由于可变模版参数的类型和个数是不固定的，所以我们可以传任意类型和个数的参数给函数f。

这个例子只是简单的将可变模版参数的个数打印出来，如果我们需要将参数包中的每个参数打印出来的话就需要通过一些方法了。展开可变模版参数函数的方法一般有两种：

是通过递归函数来展开参数包
是通过逗号表达式来展开参数包。

####### 递归函数方式展开参数包
通过递归函数展开参数包，需要提供一个参数包展开的函数和一个递归终止函数，递归终止函数正是用来终止递归的，

#include <iostream>
using namespace std;
//递归终止函数
void print()
{
   cout << "empty" << endl;
}

//展开函数
template <class T, class ...Args>
void print(T head, Args... rest)
{
   cout << "parameter " << head << endl;
   print(rest...);
}

int main(void)
{
   print(1,2,3,4);
   return 0;
}

上例会输出每一个参数，直到为空时输出empty。展开参数包的函数有两个，一个是递归函数，另外一个是递归终止函数，参数包Args…在展开的过程中递归调用自己，每调用一次参数包中的参数就会少一个，直到所有的参数都展开为止，当没有参数时，则调用非模板函数print终止递归过程。

递归调用的过程是这样的:

1	print(1,2,3,4);
2	print(2,3,4);
3	print(3,4);
4	print(4);
5	print();

上面的递归终止函数还可以写成这样：

template <class T>
void print(T t)
{
   cout << t << endl;
}
```cpp
print(1,2,3,4);
print(2,3,4);
print(3,4);
print(4);

当参数包展开到最后一个参数时递归为止。再看一个通过可变模版参数求和的例子：

template<typename T>
T sum(T t)
{
    return t;
}

template<typename T, typename ... Types>
T sum (T first, Types ... rest)
{
    return first + sum<T>(rest...);
}

sum(1,2,3,4); //10

sum在展开参数包的过程中将各个参数相加求和，参数的展开方式和前面的打印参数包的方式是一样的。

####### 逗号表达式展开参数包
递归函数展开参数包是一种标准做法，也比较好理解，但也有一个__缺点,就是必须要一个重载的递归终止函数__，即__必须要有一个同名的终止函数来终止递归__，这样可能会感觉稍有不便。

有没有一种更简单的方式呢？
其实还有一种方法可以不通过递归方式来展开参数包，这种方式需要__借助逗号表达式__和__初始化列表__。比如前面print的例子可以改成这样：

template <class T>
void printarg(T t)
{
   cout << t << endl;
}

template <class ...Args>
void expand(Args... args)
{
   int arr[] = {(printarg(args), 0)...};
}

expand(1,2,3,4);

这个例子将分别打印出1,2,3,4四个数字。这种展开参数包的方式，不需要通过递归终止函数，是直接在expand函数体中展开的, printarg不是一个递归终止函数，只是一个处理参数包中每一个参数的函数。

这种就地展开参数包的方式实现的关键是逗号表达式。我们知道逗号表达式会按顺序执行逗号前面的表达式，比如：

1	d = (a = b, c);

这个表达式会按顺序执行：b会先赋值给a，接着括号中的逗号表达式返回c的值，因此d将等于c。

expand函数中的逗号表达式：(printarg(args), 0)，也是按照这个执行顺序，先执行printarg(args)，再得到逗号表达式的结果0。

同时还用到了C++11的另外一个特性——初始化列表，通过初始化列表来初始化一个变长数组, {(printarg(args), 0)…}将会展开成
((printarg(arg1),0),
(printarg(arg2),0),
(printarg(arg3),0),
etc… )，
最终会创建一个元素值都为0的数组int arr[sizeof…(Args)]。
由于是逗号表达式，在创建数组的过程中会先执行逗号表达式前面的部分printarg(args)打印出参数，也就是说在构造int数组的过程中就将参数包展开了，这个数组的目的纯粹是为了在数组构造的过程展开参数包。我们可以把上面的例子再进一步改进一下，将函数作为参数，就可以支持lambda表达式了，从而可以少写一个递归终止函数了，具体代码如下：

template<class F, class... Args>void expand(const F& f, Args&&...args) 
{
  initializer_list<int>{(f(std::forward< Args>(args)),0)...};
}
expand([](int i){cout<<i<<endl;}, 1,2,3);

上面的例子将打印出每个参数，这里如果再使用C++14的新特性泛型lambda表达式的话，可以写更泛化的lambda表达式了：

1	expand([](auto i){cout<<i<<endl;}, 1,2.0,”test”);

可变模版参数类

可变参数模板类是一个带可变模板参数的模板类，比如C++11中的元祖std::tuple就是一个可变模板类，它的定义如下：

1	template< class... Types >
2	class tuple;

这个可变参数模板类可以携带任意类型任意个数的模板参数：

1	std::tuple<int> tp1 = std::make_tuple(1);
2	std::tuple<int, double> tp2 = std::make_tuple(1, 2.5);
3	std::tuple<int, double, string> tp3 = std::make_tuple(1, 2.5, "");

可变参数模板的模板参数个数可以为0个，所以下面的定义也是也是合法的：

1	std::tuple<> tp;

可变参数模板类的参数包展开的方式和可变参数模板函数的展开方式不同，
可变参数模板类的参数包展开需要通过__模板特化__和__继承__方式去展开，展开方式比可变参数模板函数要复杂。下面我们来看一下展开可变模版参数类中的参数包的方法。

####### 模版偏特化和递归方式来展开参数包
可变参数模板类的展开一般需要定义两到三个类，包括__类声明__和__偏特化的模板类__。
如下方式定义了一个基本的可变参数模板类：

//前向声明
template<typename... Args>
struct Sum;

//基本定义
template<typename First, typename... Rest>
struct Sum<First, Rest...>
{
    enum { value = Sum<First>::value + Sum<Rest...>::value };
};

//递归终止
template<typename Last>
struct Sum<Last>
{
    enum { value = sizeof (Last) };
};

这个Sum类的作用是在编译期计算出参数包中参数类型的size之和，通过sum<int,double,short>::value就可以获取这3个类型的size之和为14。这是一个简单的通过可变参数模板类计算的例子，可以看到一个基本的可变参数模板应用类由三部分组成。

第一部分是：它是前向声明，声明这个sum类是一个可变参数模板类；

1	template<typename... Args> struct sum

第二部分是类的定义：
它定义了一个部分展开的可变模参数模板类，告诉编译器如何递归展开参数包。

template<typename First, typename... Rest>
struct Sum<First, Rest...>
{
    enum { value = Sum<First>::value + Sum<Rest...>::value };
};

第三部分是特化的递归终止类：

1	template<typename Last> struct sum<last>
2	{
3	enum { value = sizeof (First) };
4	}

通过这个特化的类来终止递归：

1	template<typename First, typename... Args>struct sum;

这个前向声明要求sum的模板参数至少有一个，因为可变参数模板中的模板参数可以有0个，有时候0个模板参数没有意义，就可以通过上面的声明方式来限定模板参数不能为0个。
上面的这种三段式的定义也可以改为两段式的，可以将前向声明去掉，这样定义：

template<typename First, typename... Rest>
struct Sum
{
    enum { value = Sum<First>::value + Sum<Rest...>::value };
};

template<typename Last>
struct Sum<Last>
{
    enum{ value = sizeof(Last) };
};

上面的方式只要一个基本的模板类定义和一个特化的终止函数就行了，而且限定了模板参数至少有一个。递归终止模板类可以有多种写法，比如上例的递归终止模板类还可以这样写：

template<typename... Args> struct sum;
template<typename First, typenameLast>
struct sum<First, Last>
{
    enum{ value = sizeof(First) +sizeof(Last) };
};

在展开到最后两个参数时终止。
还可以在展开到0个参数时终止：

1	template<>struct sum<> { enum{ value = 0 }; };

还可以使用std::integral_constant来消除枚举定义value。
利用std::integral_constant可以获得编译期常量的特性，可以将前面的sum例子改为这样：

//前向声明
template<typename First, typename... Args>
struct Sum;

//基本定义
template<typename First, typename... Rest>
struct Sum<First, Rest...> : std::integral_constant<int, Sum<First>::value + Sum<Rest...>::value>
{
};

//递归终止
template<typename Last>
struct Sum<Last> : std::integral_constant<int, sizeof(Last)>
{
};
sum<int,double,short>::value;//值为14

####### 继承方式展开参数包
还可以通过继承方式来展开参数包，比如下面的例子就是通过继承的方式去展开参数包：

//整型序列的定义
template<int...>
struct IndexSeq{};

//继承方式，开始展开参数包
template<int N, int... Indexes>
struct MakeIndexes : MakeIndexes<N - 1, N - 1, Indexes...> {};

// 模板特化，终止展开参数包的条件
template<int... Indexes>
struct MakeIndexes<0, Indexes...>
{
    typedefIndexSeq<Indexes...> type;
};

int main()
{
    using T = MakeIndexes<3>::type;
    cout <<typeid(T).name() << endl;
    return 0;
}

其中MakeIndexes的作用是为了生成一个可变参数模板类的整数序列，最终输出的类型是：struct IndexSeq<0,1,2>。

MakeIndexes继承于自身的一个特化的模板类，这个特化的模板类同时也在展开参数包，这个展开过程是通过继承发起的，直到遇到特化的终止条件展开过程才结束。
MakeIndexes<1,2,3>::type的展开过程是这样的：

MakeIndexes<3> : MakeIndexes<2, 2>{}
MakeIndexes<2, 2> : MakeIndexes<1, 1, 2>{}
MakeIndexes<1, 1, 2> : MakeIndexes<0, 0, 1, 2>
{
    typedef IndexSeq<0, 1, 2> type;
}

通过不断的继承递归调用，最终得到整型序列IndexSeq<0, 1, 2>。
如果不希望通过继承方式去生成整形序列，则可以通过下面的方式生成。

template<int N, int... Indexes>
struct MakeIndexes3
{
    using type = typename MakeIndexes3<N - 1, N - 1, Indexes...>::type;
};

template<int... Indexes>
struct MakeIndexes3<0, Indexes...>
{
    typedef IndexSeq<Indexes...> type;
};

我们看到了如何利用递归以及偏特化等方法来展开可变模版参数，下面来看看可变模版参数的一些应用。

可变参数模版消除重复代码

C++11之前如果要写一个泛化的工厂函数，这个工厂函数能接受任意类型的入参，并且参数个数要能满足大部分的应用需求的话，我们不得不定义很多重复的模版定义，比如下面的代码：

template<typename T>
T* Instance()
{
    return new T();
}

template<typename T, typename T0>
T* Instance(T0 arg0)
{
    return new T(arg0);
}

template<typename T, typename T0, typename T1>
T* Instance(T0 arg0, T1 arg1)
{
    return new T(arg0, arg1);
}

template<typename T, typename T0, typename T1, typename T2>
T* Instance(T0 arg0, T1 arg1, T2 arg2)
{
    return new T(arg0, arg1, arg2);
}

template<typename T, typename T0, typename T1, typename T2, typename T3>
T* Instance(T0 arg0, T1 arg1, T2 arg2, T3 arg3)
{
    return new T(arg0, arg1, arg2, arg3);
}

template<typename T, typename T0, typename T1, typename T2, typename T3, typename T4>
T* Instance(T0 arg0, T1 arg1, T2 arg2, T3 arg3, T4 arg4)
{
    return new T(arg0, arg1, arg2, arg3, arg4);
}
struct A
{
    A(int){}
};

struct B
{
    B(int,double){}
};
A* pa = Instance<A>(1);
B* pb = Instance<B>(1,2);

可以看到这个泛型工厂函数存在大量的重复的模板定义，并且限定了模板参数。
通过可变参数模版优化后的工厂函数如下：

template<typename…  Args>
T* Instance(Args&&… args)
{
    return new T(std::forward<Args>(args)…);
}
A* pa = Instance<A>(1);
B* pb = Instance<B>(1,2);

可变参数模版实现泛化的delegate

C++中没有类似C#的委托，我们可以借助可变模版参数来实现一个。C#中的委托的基本用法是这样的：

delegate int AggregateDelegate(int x, int y);//声明委托类型

int Add(int x, int y){return x+y;}
int Sub(int x, int y){return x-y;}

AggregateDelegate add = Add;
add(1,2);//调用委托对象求和
AggregateDelegate sub = Sub;
sub(2,1);// 调用委托对象相减

C#中的委托的使用需要先定义一个委托类型，这个委托类型不能泛化，即委托类型一旦声明之后就不能再用来接受其它类型的函数了，比如这样用：

1	int Fun(int x, int y, int z){return x+y+z;}
2	int Fun1(string s, string r){return s.Length+r.Length; }
3	AggregateDelegate fun = Fun; //编译报错，只能赋值相同类型的函数
4	AggregateDelegate fun1 = Fun1;//编译报错，参数类型不匹配

这里不能泛化的原因是声明委托类型的时候就限定了参数类型和个数，在C11不存在这个问题了。因为有了可变模版参数，它就代表了任意类型和个数的参数了，下面让我们来看一下如何实现一个功能更加泛化的C版本的委托（这里为了简单起见只处理成员函数的情况，并且忽略const、volatile和const volatile成员函数的处理）。

template <class T, class R, typename... Args>
class  MyDelegate
{
public:
    MyDelegate(T* t, R  (T::*f)(Args...) ):m_t(t),m_f(f) {}

    R operator()(Args&&... args) 
    {
            return (m_t->*m_f)(std::forward<Args>(args) ...);
    }

private:
    T* m_t;
    R  (T::*m_f)(Args...);
};   

template <class T, class R, typename... Args>
MyDelegate<T, R, Args...> CreateDelegate(T* t, R (T::*f)(Args...))
{
    return MyDelegate<T, R, Args...>(t, f);
}

struct A
{
    void Fun(int i){cout<<i<<endl;}
    void Fun1(int i, double j){cout<<i+j<<endl;}
};

int main()
{
    A a;
    auto d = CreateDelegate(&a, &A::Fun); //创建委托
    d(1); //调用委托，将输出1
    auto d1 = CreateDelegate(&a, &A::Fun1); //创建委托
    d1(1, 2.5); //调用委托，将输出3.5
}

MyDelegate实现的关键是内部定义了一个能接受任意类型和个数参数的“万能函数”：R (T::*m_f)(Args…)，正是由于可变模版参数的特性，所以我们才能够让这个m_f接受任意参数。

编译期获取最大值

//获取最大的整数
template <size_t arg, size_t... rest>
struct IntegerMax;

template <size_t arg>
struct IntegerMax<arg> : std::integral_constant<size_t, arg>
{
};

template <size_t arg1, size_t arg2, size_t... rest>
struct IntegerMax<arg1, arg2, rest...> : std::integral_constant<size_t, arg1 >= arg2 ? IntegerMax<arg1, rest...>::value :
    IntegerMax<arg2, rest...>::value >
{
};

这个IntegerMax的实现用到了type_traits中的std::integral_const，它在展开参数包的过程中，不断的比较，直到所有的参数都比较完，最终std::integral_const的value值即为最大值。它的使用很简单：

1	cout << IntegerMax<2, 5, 1, 7, 3>::value << endl; //value为7

我们可以在IntegerMax的基础上轻松的实现获取最大内存对齐值的元函数MaxAlign。

编译期获取最大的align

template<typename... Args>
struct MaxAlign : std::integral_constant<int, IntegerMax<std::alignment_of<Args>::value...>::value>{};
cout << MaxAlign<int, short, double, char>::value << endl; //value为8

//编译判断是否包含了某种类型：
template < typename T, typename... List >
struct Contains;

template < typename T, typename Head, typename... Rest >
struct Contains<T, Head, Rest...>
    : std::conditional< std::is_same<T, Head>::value, std::true_type, Contains<T, Rest... >> ::type{};

template < typename T >
struct Contains<T> : std::false_type{};
//用法：
cout<<Contains<int, char, double, int, short>::value<<endl; //输出true

这个Contains的实现用到了type_traits的std::conditional、std::is_same、std::true_type和std::false_type，它的实现思路是在展开参数包的过程中不断的比较类型是否相同，如果相同则设置值为true，否则设置为false。

编译期获取类型的索引

template < typename T, typename... List >
struct IndexOf;

template < typename T, typename Head, typename... Rest >
struct IndexOf<T, Head, Rest...>
{
    enum{ value = IndexOf<T, Rest...>::value+1 };
};

template < typename T, typename... Rest >
struct IndexOf<T, T, Rest...>
{
    enum{ value = 0 };
};

template < typename T >
struct IndexOf<T>
{
    enum{value = -1};
};

//用法：
cout<< IndexOf<int, double, short, char, int, float>::value<<endl; //输出3

这个IndexOf的实现比较简单，在展开参数包的过程中看是否匹配到特化的IndexOf<T, T, Rest…>，如果匹配上则终止递归将之前的value累加起来得到目标类型的索引位置，否则将value加1，如果所有的类型中都没有对应的类型则返回-1；

编译期根据索引位置查找类型

template<int index, typename... Types>
struct At;

template<int index, typename First, typename... Types>
struct At<index, First, Types...>
{
    using type = typename At<index - 1, Types...>::type;
};

template<typename T, typename... Types>
struct At<0, T, Types...>
{
    using type = T;
};

//用法：
using T = At<1, int, double, char>::type;
cout << typeid(T).name() << endl; //输出double

At的实现比较简单，只要在展开参数包的过程中，不断的将索引递减至0时为止即可获取对应索引位置的类型。

编译期遍历类型。

template<typename T>
void printarg()
{
    cout << typeid(T).name() << endl;
}

template<typename... Args>
void for_each() 
{
    std::initializer_list<int>{(printarg<Args>(), 0)...};
}
//用法：
for_each<int,double>();//将输出int double

这里for_each的实现是通过初始化列表和逗号表达式来遍历可变模板参数的。

可以看到，借助__可变模板参数__和__type_traits__以及__模板偏特化__和__递归等方式__我们可以实现一些有用的编译期算法。这些算法为我们编写应用层级别的代码奠定了基础，后面模板元编程的具体应用中将会用到这些元函数。

tuple与模版元

C++11的tuple本身就是一个可变模板参数组成的元函数，它的原型如下：

1	template<class...Types>
2	class tuple;

tuple在模版元编程中的一个应用场景是将可变模板参数保存起来，因为可变模板参数不能直接作为变量保存起来，需要借助tuple保存起来，保存之后再在需要的时候通过一些手段将tuple又转换为可变模板参数。这个过程有点类似于化学中的“氧化还原反应”。

看看下面的例子中，可变模板参数和tuple是如何相互转换的：

//定义整形序列
template<int...>
struct IndexSeq{};

//生成整形序列
template<int N, int... Indexes>
struct MakeIndexes : MakeIndexes<N - 1, N - 1, Indexes...>{};

template<int... indexes>
struct MakeIndexes<0, indexes...>{
    typedef IndexSeq<indexes...> type;
};

template<typename... Args>
void printargs(Args... args){
    //先将可变模板参数保存到tuple中
    print_helper(typename MakeIndexes<sizeof... (Args)>::type(), std::make_tuple(args...));
}

template<int... Indexes, typename... Args>
void print_helper(IndexSeq<Indexes...>, std::tuple<Args...>&& tup){
    //再将tuple转换为可变模板参数，将参数还原回来，再调用print
    print(std::get<Indexes>(tup)...); 
}
template<typename T>
void print(T t)
{
    cout << t << endl;
}

template<typename T, typename... Args>
void print(T t, Args... args)
{
    print(t);
    print(args...);
}

输出:

1	printargs(1, 2.5, “test”); //将输出1 2.5 test

上面的例子print实际上是输出可变模板参数的内容，具体做法是

将可变模板参数保存到tuple中
通过元函数MakeIndexes生成一个整形序列，这个整形序列就是IndexSeq<0,1,2>
整形序列代表了tuple中元素的索引，
生成整形序列之后再调用print_helper，在print_helper中展开这个整形序列
展开的过程中根据具体的索引从tuple中获取对应的元素，
最终将从tuple中取出来的元素组成一个可变模板参数，从而实现了tuple“还原”为可变模板参数
最终调用print打印可变模板参数。

tuple在模板元编程中的另外一个应用场景是用来实现一些编译期算法，比如常见的遍历、查找和合并等算法，实现的思路和可变模板参数实现的编译期算法类似。

模版元实现function_traits

function_traits用来获取函数语义的可调用对象的一些属性，比如函数类型、返回类型、函数指针类型和参数类型等。下面来看看如何实现function_traits

template<typename T>
struct function_traits;

//普通函数
template<typename Ret, typename... Args>
struct function_traits<Ret(Args...)>
{
public:
    enum { arity = sizeof...(Args) };
    typedef Ret function_type(Args...);
    typedef Ret return_type;
    using stl_function_type = std::function<function_type>;
    typedef Ret(*pointer)(Args...);

    template<size_t I>
    struct args
    {
        static_assert(I < arity, "index is out of range, index must less than sizeof Args");
        using type = typename std::tuple_element<I, std::tuple<Args...>>::type;
    };
};

//函数指针
template<typename Ret, typename... Args>
struct function_traits<Ret(*)(Args...)> : function_traits<Ret(Args...)>{};

//std::function
template <typename Ret, typename... Args>
struct function_traits<std::function<Ret(Args...)>> : function_traits<Ret(Args...)>{};

//member function
#define FUNCTION_TRAITS(...) \
    template <typename ReturnType, typename ClassType, typename... Args>\
    struct function_traits<ReturnType(ClassType::*)(Args...) __VA_ARGS__> : function_traits<ReturnType(Args...)>{}; \

FUNCTION_TRAITS()
FUNCTION_TRAITS(const)
FUNCTION_TRAITS(volatile)
FUNCTION_TRAITS(const volatile)

//函数对象
template<typename Callable>
struct function_traits : function_traits<decltype(&Callable::operator())>{};

由于可调用对象可能是普通的函数、函数指针、lambda、std::function和成员函数，所以我们需要针对这些类型分别做偏特化，然后萃取出可调用对象的元信息。

其中，成员函数的偏特化稍微复杂一点，因为涉及到cv符的处理，这里通过定义一个宏来消除重复的模板类定义。参数类型的获取我们是借助于tuple，将参数转换为tuple类型，然后根据索引来获取对应类型。它的用法比较简单：

template<typename T>
void PrintType()
{
    cout << typeid(T).name() << endl;
}

int main()
{
    std::function<int(int)> f = [](int a){return a; };

    //打印函数类型
    PrintType<function_traits<std::function<int(int)>>::function_type>(); //将输出int __cdecl(int)

    //打印函数的第一个参数类型
    PrintType<function_traits<std::function<int(int)>>::args<0>::type>();//将输出int

    //打印函数的返回类型
    PrintType<function_traits<decltype(f)>::return_type>(); //将输出int

　　//打印函数指针类型
    PrintType<function_traits<decltype(f)>::pointer>(); //将输出int (__cdecl*)(int)
}

可以看到这个function_traits通过类型萃取，可以很方便地获取可调用对象（函数、函数指针、函数对象、std::function和lambda表达式）的一些元信息，功能非常强大，这个function_traits经常会用到是更高层模版元程序的基础。

比如Variant类型的实现就要用到这个function_traits，下面来看看Variant的实现。

模版元实现Vairant类型

借助上面的function_traits和前文实现的一些元函数，我们就能方便的实现一个“万能类型”—Variant，Variant实际上一个泛化的类型，这个Variant需要预定义一些类型作为可接受的类型。

通过C++11模版元实现的Variant将改进值的获取，将获取实际值的方式改为内置的，即通过下面的方式来访问：

typedef Variant<int, double, string, int> cv;

cv v = 10;

v.Visit([&](double i){cout << i << endl; }, [](short i){cout << i << endl; }, [=](int i){cout << i << endl; },[](const string& i){cout << i << endl; });//结果将输出10

Variant完整实现

#include <typeindex>
#include <iostream>

/** 获取最大的整数 */
template <size_t arg, size_t... rest>
struct IntegerMax;

template <size_t arg>
struct IntegerMax<arg> : std::integral_constant<size_t, arg>
{
};

template <size_t arg1, size_t arg2, size_t... rest>
struct IntegerMax<arg1, arg2, rest...> : std::integral_constant<size_t, arg1 >= arg2 ? IntegerMax<arg1, rest...>::value 
    : IntegerMax<arg2, rest...>::value>
{
};

/** 获取最大的align */
template<typename... Args>
struct MaxAlign : std::integral_constant<int, IntegerMax<std::alignment_of<Args>::value...>::value>
{
};

/** 是否包含某个类型 */
template <typename T, typename... List>
struct Contains;

template <typename T, typename Head, typename... Rest>
struct Contains<T, Head, Rest...>
	: std::conditional<std::is_same<T, Head>::value, std::true_type, Contains<T, Rest... >> ::type
{
};

template <typename T>
struct Contains<T> : std::false_type
{
};

template <typename T, typename... List>
struct IndexOf;

template <typename T, typename Head, typename... Rest>
struct IndexOf<T, Head, Rest...>
{
	enum { value = IndexOf<T, Rest...>::value + 1 };
};

template <typename T, typename... Rest>
struct IndexOf<T, T, Rest...>
{
	enum { value = 0 };
};

template <typename T>
struct IndexOf<T>
{
	enum{value = -1};
};

template<int index, typename... Types>
struct At;

template<int index, typename First, typename... Types>
struct At<index, First, Types...>
{
	using type = typename At<index - 1, Types...>::type;
};

template<typename T, typename... Types>
struct At<0, T, Types...>
{
	using type = T;
};

template<typename... Types>
class Variant
{
	enum
	{
		data_size = IntegerMax<sizeof(Types)...>::value,
		align_size = MaxAlign<Types...>::value
	};
	using data_t = typename std::aligned_storage<data_size, align_size>::type;
public:
	template<int index>
	using IndexType = typename At<index, Types...>::type;

	Variant(void) :type_index_(typeid(void))
	{
	}

	~Variant()
	{
		destroy(type_index_, &data_);
	}

	Variant(Variant<Types...>&& old) : type_index_(old.type_index_)
	{
		move(old.type_index_, &old.data_, &data_);
	}

	Variant(const Variant<Types...>& old) : type_index_(old.type_index_)
	{
		copy(old.type_index_, &old.data_, &data_);
	}

	Variant& operator=(const Variant& old)
	{
		copy(old.type_index_, &old.data_, &data_);
		type_index_ = old.type_index_;
		return *this;
	}

	Variant& operator=(Variant&& old)
	{
		move(old.type_index_, &old.data_, &data_);
		type_index_ = old.type_index_;
		return *this;
	}

	template <class T,
	class = typename std::enable_if<Contains<typename std::decay<T>::type, Types...>::value>::type>
		Variant(T&& value) : type_index_(typeid(void))
	{
			destroy(type_index_, &data_);
			typedef typename std::decay<T>::type U;
			new(&data_) U(std::forward<T>(value));
			type_index_ = std::type_index(typeid(U));
	}

	template<typename T>
	bool is() const
	{
		return (type_index_ == std::type_index(typeid(T)));
	}

	bool Empty() const
	{
		return type_index_ == std::type_index(typeid(void));
	}

	std::type_index type() const
	{
		return type_index_;
	}

	template<typename T>
	typename std::decay<T>::type& get()
	{
		using U = typename std::decay<T>::type;
		if (!is<U>())
		{
			std::cout << typeid(U).name() << " is not defined. " 
                << "current type is " << type_index_.name() << std::endl;
			throw std::bad_cast{};
		}

		return *(U*)(&data_);
	}

	template <typename T>
	int indexOf()
	{
		return IndexOf<T, Types...>::value;
	}

	bool operator==(const Variant& rhs) const
	{
		return type_index_ == rhs.type_index_;
	}

	bool operator<(const Variant& rhs) const
	{
		return type_index_ < rhs.type_index_;
	}

private:
	void destroy(const std::type_index& index, void *buf)
	{
        [](Types&&...){}((destroy0<Types>(index, buf), 0)...);
	}

	template<typename T>
	void destroy0(const std::type_index& id, void *data)
	{
		if (id == std::type_index(typeid(T)))
			reinterpret_cast<T*>(data)->~T();
	}

	void move(const std::type_index& old_t, void *old_v, void *new_v) 
	{
        [](Types&&...){}((move0<Types>(old_t, old_v, new_v), 0)...);
	}

	template<typename T>
	void move0(const std::type_index& old_t, void *old_v, void *new_v)
	{
		if (old_t == std::type_index(typeid(T)))
			new (new_v)T(std::move(*reinterpret_cast<T*>(old_v)));
	}

	void copy(const std::type_index& old_t, const void *old_v, void *new_v)
	{
        [](Types&&...){}((copy0<Types>(old_t, old_v, new_v), 0)...);
	}

	template<typename T>
	void copy0(const std::type_index& old_t, const void *old_v, void *new_v)
	{
		if (old_t == std::type_index(typeid(T)))
			new (new_v)T(*reinterpret_cast<const T*>(old_v));
	}

private:
	data_t data_;
	std::type_index type_index_;
};

实现Variant首先需要定义一个足够大的缓冲区用来存放不同的类型的值，这个缓类型冲区实际上就是用来擦除类型，不同的类型都通过placement new在这个缓冲区上创建对象，因为类型长度不同，所以需要考虑内存对齐，C++11刚好提供了内存对齐的缓冲区aligned_storage：

1	template< std::size_t Len, std::size_t Align = /default-alignment/ >
2	struct aligned_storage;

它的第一个参数是缓冲区的长度，第二个参数是缓冲区内存对齐的大小，由于Varaint可以接受多种类型，所以我们需要获取最大的类型长度，保证缓冲区足够大，然后还要获取最大的内存对齐大小，这里我们通过前面实现的MaxInteger和MaxAlign就可以了，Varaint中内存对齐的缓冲区定义如下：

enum
{
        data_size = IntegerMax<sizeof(Types)...>::value,
        align_size = MaxAlign<Types...>::value
};

using data_t = typename std::aligned_storage<data_size, align_size>::type; //内存对齐的缓冲区类型

其次，我们还要实现对缓冲区的构造、拷贝、析构和移动，因为Variant重新赋值的时候需要将缓冲区中原来的类型析构掉，拷贝构造和移动构造时则需要拷贝和移动。这里以析构为例，我们需要根据当前的type_index来遍历Variant的所有类型，找到对应的类型然后调用该类型的析构函数。

void Destroy(const type_index& index, void * buf)
{
	std::initializer_list<int>{(Destroy0<Types>(index, buf), 0)...};
}

template<typename T>
void Destroy0(const type_index& id, void* data)
{
	if (id == type_index(typeid(T)))
		reinterpret_cast<T*>(data)->~T();
}

这里，我们通过初始化列表和逗号表达式来展开可变模板参数，在展开的过程中查找对应的类型，如果找到了则析构。在Variant构造时还需要注意一个细节是，Variant不能接受没有预先定义的类型，所以在构造Variant时，需要限定类型必须在预定义的类型范围当中，这里通过type_traits的enable_if来限定模板参数的类型。

template <class T,
		class = typename std::enable_if<Contains<typename std::remove_reference<T>::type, Types...>::value>::type> Variant(T&& value) : m_typeIndex(typeid(void)) {
            Destroy(m_typeIndex, &m_data);
            typedef typename std::remove_reference<T>::type U;
            new(&m_data) U(std::forward<T>(value));
            m_typeIndex = type_index(typeid(U));
    }

这里enbale_if的条件就是前面实现的元函数Contains的值，当没有在预定义的类型中找到对应的类型时，即Contains返回false时，编译期会报一个编译错误。

最后还需要实现内置的Vistit功能，Visit的实现需要先通过定义一系列的访问函数，然后再遍历这些函数，遍历过程中，判断函数的第一个参数类型的type_index是否与当前的type_index相同，如果相同则获取当前类型的值。

template<typename F>
void Visit(F&& f){
	using T = typename Function_Traits<F>::template arg<0>::type;
	if (Is<T>())
		f(Get<T>());
}

template<typename F, typename... Rest>
void Visit(F&& f, Rest&&... rest){
	using T = typename Function_Traits<F>::template arg<0>::type;
	if (Is<T>())
		Visit(std::forward<F>(f));
	else
		Visit(std::forward<Rest>(rest)...);
}

Visit功能的实现利用了可变模板参数和function_traits，通过可变模板参数来遍历一系列的访问函数，遍历过程中，通过function_traits来获取第一个参数的类型，和Variant当前的type_index相同时则取值。

为什么要获取访问函数第一个参数的类型呢？因为Variant的值是唯一的，只有一个值，所以获取的访问函数的第一个参数的类型就是Variant中存储的对象的实际类型。

模版元实现bind

C++11中新增的std::bind是一个很灵活且功能强大的绑定器，std::bind用来将可调用对象与其参数进行绑定。绑定后的结果可以使用std::function进行保存，并延迟调用到任何我们需要的时候。
下面是它的基本用法：

void output(int x, int y)
{
    std::cout << x << " " << y << std::endl;
}

int main(void)
{
    std::bind(output, 1, 2)();                          // 输出: 1 2
    std::bind(output, std::placeholders::_1, 2)(1);     // 输出: 1 2
    std::bind(output, 2, std::placeholders::_1)(1);     // 输出: 2 1
}

std:: placeholders::_1是一个占位符，代表这个位置将在函数调用时，被传入的第一个参数所替代。因为有了占位符的概念，std::bind的使用非常灵活，我们可以用它来替代任意位置的参数，延迟到后面再传入实际参数。bind的原理图:

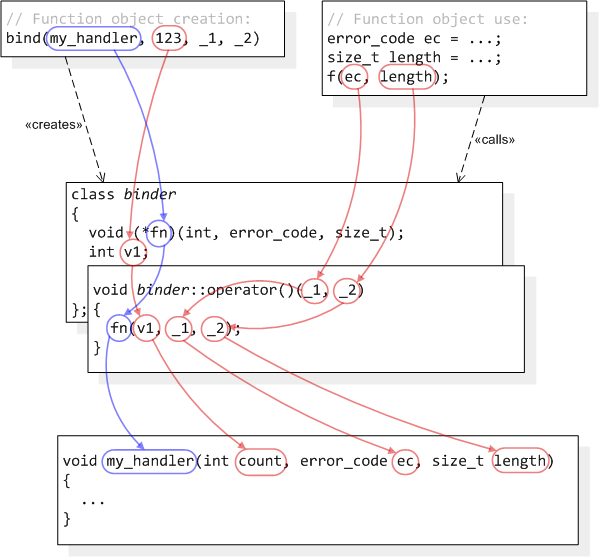
从上图中可以看到bind把参数和占位符保存起来了，然后在后面调用的时候再按照顺序去替换占位符，最终实现延迟执行。

我们可以通过模板元来实现一个简单的bind，实现bind需要解决两个问题：

将tuple展开为可变模板参数
bind绑定可调用对象时，需要将可调用对象的形参（可能含占位符）保存起来，保存到tuple中了。到了调用阶段，我们就要反过来将tuple展开为可变参数，因为这个可变参数才是可调用对象的形参，否则就无法实现调用了。这里我们会借助于一个整形序列来将tuple变为可变参数，在展开tuple的过程中我们还需要根据占位符来选择合适实参，即占位符要替换为调用实参。这里要用到前文中实现的MakeIndexes。
根据占位符来选择合适的实参
这个地方比较关键，因为tuple中可能含有占位符，我们展开tuple时，如果发现某个元素类型为占位符，则从调用的实参生成的tuple中取出一个实参，用来作为变参的一个参数；当某个类型不为占位符时，则直接从绑定时生成的形参tuple中取出参数，用来作为变参的一个参数。最终tuple被展开为一个变参列表，这时，这个列表中没有占位符了，全是实参，就可以实现调用了。这里还有一个细节要注意，替换占位符的时候，如何从tuple中选择合适的参数呢，因为替换的时候要根据顺序来选择。这里是通过占位符的模板参数I来选择，因为占位符place_holder的实例_1实际上place_holder<1>, 占位符实例_2实际上是palce_holder<2>,我们是可以根据占位符的模板参数来获取其顺序的。

#include <tuple>
#include <type_traits>
using namespace std;

template<int...>
struct IndexTuple{};

template<int N, int... Indexes>
struct MakeIndexes : MakeIndexes<N - 1, N - 1, Indexes...>{};

template<int... indexes>
struct MakeIndexes<0, indexes...>
{
    typedef IndexTuple<indexes...> type;
};

template <int I>
struct Placeholder
{
};

Placeholder<1> _1; Placeholder<2> _2; Placeholder<3> _3; Placeholder<4> _4; Placeholder<5> _5; 
Placeholder<6> _6; Placeholder<7> _7;Placeholder<8> _8; Placeholder<9> _9; Placeholder<10> _10;

// result type traits
template <typename F>
struct result_traits : result_traits<decltype(&F::operator())> {};

template <typename T>
struct result_traits<T*> : result_traits<T> {};

/* check function */

template <typename R, typename... P>
struct result_traits<R(*)(P...)> { typedef R type; };

/* check member function */
template <typename R, typename C, typename... P> 
struct result_traits<R(C::*)(P...)> { typedef R type; };

template <typename T, class Tuple>
inline auto select(T&& val, Tuple&)->T&&
{
    return std::forward<T>(val);
}

template <int I, class Tuple>
inline auto select(Placeholder<I>&, Tuple& tp) -> decltype(std::get<I - 1>(tp))
{
    return std::get<I - 1>(tp);
}

// The invoker for call a callable
template <typename T>
struct is_pointer_noref
    : std::is_pointer<typename std::remove_reference<T>::type>
{};

template <typename T>
struct is_memfunc_noref
    : std::is_member_function_pointer<typename std::remove_reference<T>::type>
{};

template <typename R, typename F, typename... P>
inline typename std::enable_if<is_pointer_noref<F>::value,
R>::type invoke(F&& f, P&&... par)
{
    return (*std::forward<F>(f))(std::forward<P>(par)...);
}

template <typename R, typename F, typename P1, typename... P>
inline typename std::enable_if<is_memfunc_noref<F>::value && is_pointer_noref<P1>::value,
R>::type invoke(F&& f, P1&& this_ptr, P&&... par)
{
    return (std::forward<P1>(this_ptr)->*std::forward<F>(f))(std::forward<P>(par)...);
}

template <typename R, typename F, typename P1, typename... P>
inline typename std::enable_if<is_memfunc_noref<F>::value && !is_pointer_noref<P1>::value,
R>::type invoke(F&& f, P1&& this_obj, P&&... par)
{
    return (std::forward<P1>(this_obj).*std::forward<F>(f))(std::forward<P>(par)...);
}

template <typename R, typename F, typename... P>
inline typename std::enable_if<!is_pointer_noref<F>::value && !is_memfunc_noref<F>::value,
R>::type invoke(F&& f, P&&... par)
{
    return std::forward<F>(f)(std::forward<P>(par)...);
}

template<typename Fun, typename... Args>
struct Bind_t
{
    typedef typename decay<Fun>::type FunType;
    typedef std::tuple<typename decay<Args>::type...> ArgType;

    typedef typename result_traits<FunType>::type     result_type;
public:
    template<class F, class... BArgs>
    Bind_t(F& f,  BArgs&... args) : m_func(f), m_args(args...)
    {
    }

    template<typename F, typename... BArgs>
    Bind_t(F&& f, BArgs&&... par) : m_func(std::move(f)), m_args(std::move(par)...)
    {}

    template <typename... CArgs>
    result_type operator()(CArgs&&... args)
    {
        return do_call(MakeIndexes<std::tuple_size<ArgType>::value>::type(), 
std::forward_as_tuple(std::forward<CArgs>(args)...));
    }

    template<typename ArgTuple, int... Indexes >
    result_type do_call(IndexTuple< Indexes... >& in, ArgTuple& argtp)
    {
        return simple::invoke<result_type>(m_func, select(std::get<Indexes>(m_args), 
argtp)...);
        //return m_func(select(std::get<Indexes>(m_args), argtp)...);
    }

private:
    FunType m_func;
    ArgType m_args;
};

template <typename F, typename... P>
inline Bind_t<F, P...> Bind(F&& f, P&&... par)
{
    return Bind_t<F, P...>(std::forward<F>(f), std::forward<P>(par)...);
}

template <typename F, typename... P>
inline Bind_t<F, P...> Bind(F& f, P&... par)
{
    return Bind_t<F, P...>(f, par...);
}

由于只是展示bind实现的关键技术，很多的实现细节并没有处理，比如参数是否是引用、右值、cv符、绑定非静态的成员变量都还没处理，仅仅用来展示如何综合运用一些模版元技巧和元函数，并非是重复发明轮子，只是展示bind是如何实现, 实际项目中还是使用c++11的std::bind为好。

智能指针

在管理动态分配的内存时，一个最棘手的问题就是决定何时释放这些内存，而智能指针就是用来简化内存管理的编程方式。智能指针一般有独占和共享两种所有权模型。

holder和trule两种智能指针类型：

holder类型独占一个对象；
trule可以使对象的拥有者从一个holder传递给另一个holder。

holder

智能指针会在下面两种情况下释放所指向的对象：

本身被释放
把另一个指针赋值给它

下面我们模拟实现一个智能指针：

1	template<typename T>
2	class Holder
3	{
4	private:
5	T* ptr; // 引用它所持有的对象（前提是该对象存在）
6	public:
7	// 缺省构造函数：让该holder引用一个空对象
8	Holder() : ptr(0) { }
9
10	// 针对指针的构造函数：让该holder引用该指针所指向的对象
11	// 这里使用explicit，禁止隐式转型(也即禁止了使用赋值语法来初始化Holder对象，如“holderObj = originObj”形式的赋值语法)
12	// 但依然可以通过对象构造的形式来给对象初始化，如"Holder holderObj(originObj)"，这里是显式转型。
13	explicit Holder (T* p) : ptr(p) {}
14
15	// 析构函数：释放所引用的对象（前提是该对象存在）
16	~Holder() {
17	delete ptr;
18	}
19
20	// 针对新指针的赋值运算符
21	Holder<T>& operator= (T* p){
22	delete ptr;
23	ptr = p;
24	return *this;
25	}
26
27	// 指针运算符
28	T& operator* () const {
29	return *ptr;
30	}
31
32	T* operator-> () const {
33	return ptr;
34	}
35
36	// 获取所引用的对象（前提是该对象存在）
37	T* get() const {
38	return ptr;
39	}
40
41	// 释放对所引用对象的所有权
42	void release() {
43	ptr = 0;
44	}
45
46	// 与另一个holder交换所有权
47	void exchange_with(Holder<T>& h) {
48	swap(ptr, h.ptr);
49	}
50
51	// 与其他的指针交换所有权
52	void exchange_twith(T*& p) { // 参数是什么语法？传入指针p的引用？
53	swap(ptr, p);
54	}
55
56	private:
57	// 不想外提供拷贝构造函数和拷贝赋值运算符
58	// 不允许一个Holder对象A赋值给另一个Holder对象B.
59	Holder(Holder<T> const&);
60	Holder<T>& operator= (Holder<T> const&);
61	};

从语义上讲，该holder独占ptr所引用对象的所有权。而且，这个对象一定要用new操作来创建，因为在销毁holder所拥有对象的时候，需要用到delete。

release()成员函数释放holder对其持有对象的所有权。另外，上面的普通赋值运算符也设计得比较巧妙，它会销毁和释放任何被拥有的对象，因为另一个对象会替代原先的对象被holder所拥有，而且赋值运算符也不会返回原先对象的一个holder或指针（而是返回新对象的一个holder）。

最后，我们添加了两个exchange_with()成员函数，从而可以在不销毁原有对象的前提下，方便地替换该holder所拥有的对象。
所以，我们可以如下使用上面的Holder创建两个对象：

Holder<Something> first(new Something);
firsh->perform();

Holder<Something> second(new Something);
second->perform();

作为成员的holder

我们也可以在类中使用holder来避免资源泄漏。要注意的是，只有那些完成构造之后的对象，它的析构函数才会被调用。因此，如果在构造函数内部产生异常，那么只有那些构造函数已正常执行完毕的成员对象，它的析构函数才会被调用。

#include "holder.hpp"

class RefMembers
{
    private:
        Holder<MemType> ptr1;       // 所引用的成员
        Holder<MemType> ptr2;

   public:
        // 缺省构造函数
        // - 不可能出现资源泄漏
        RefMembers() : ptr1(new MemType), ptr2(new MemType) { }

        // 拷贝构造函数
        // - 不可能出现资源泄漏
        RefMembers (RefMembers const& x) : ptr1(new MemType(*x.ptr1)), ptr2(new MemType(*x.ptr2)) { }

        // 赋值运算符
        const RefMembers& operator= (RefMembers const& x){
            *ptr1 = *x.ptr1;
            *ptr2 = *x.ptr2;
            return *this;
        }

        // 不需要析构函数
        // （缺省的析构函数将会让ptr1和ptr2删除它们所引用的对象）
        ...
};

要注意的是，我们在这里可以省略用户定义的析构函数，但一定要编写拷贝构造函数和赋值运算符

Holder所用到的基本思想是一种称为“资源获取即初始化”或RAII的模式

trule

为了解决holder在参数传递，返回值处理时的不足之处，以及复制holder、跨函数调用来复制holder所会产生的问题，引入trule。

trule: 一个专门用于传递holder的辅助类模板，并把它称为trule

1	template <typename T>
2	class Holder;
3
4	template <typename T>
5	class Trule
6	{
7	private:
8	T* ptr; // trule所引用的对象（如果有的话）
9
10	public:
11	// 构造函数，确保trule只能作为返回类型，用于将holder从被调用函数传递给调用函数
12	// 显式构造函数（会自动屏蔽默认无参构造函数），只能通过Holder构造Trule对象
13	Trule (Holder<T>& h){
14	ptr = h.get();
15	h.release();
16	}
17
18	// 拷贝构造函数
19	// trule通常是作为那些想传递holders的函数的返回类型
20	// 也就是说trule对象总是作为临时对象（rvalues，右值）出现；
21	// 因此它们的类型也就只能是常引用（reference-to-const）类型。
22	Trule (Trule<T> const& t){
23	ptr = t.ptr;
24	// 由于Trule不能作为一份拷贝，也不能含有一份拷贝，如果希望实现类似于拷贝操作，
25	// 就必须移除原trule的所有权。我们是通过将被封装指针置为空来实现这种移除操作的。
26
27	// 而最后这个置空操作显然只能针对non-const对象。
28	// 所以才有了这种把const强制转型为non-const的做法。
29	// 另外，由于原来的对象实际上并没有被定义为常类型，所以即使这样做有些别扭，
30	// 但在这种情况下这种转型却能合法地实现。
31
32	// 因此，对于最后需要把一个holder转换为trule，并且将其返回的函数，
33	// 如果要声明这类函数的返回类型，我们就必须把它声明为trule<T>类型，
34	// 而绝对不能声明为trule<T> const，这点需特别注意。
35	// 如下面例子中的函数load_something()
36	const_cast<Trule<T>&>(t).ptr = 0; // 置空操作
37	}
38
39	// 析构函数
40	~Trule() {
41	delete ptr;
42	}
43
44	private:
45	// 对于trule的用法，除了作为传递holder对象的返回类型，我们要防止把它用于其他地方。
46	// 一个接收non-const引用对象的拷贝构造函数和一个类似的拷贝赋值运算符，都被声明为私用函数，防止外界直接调用。
47	// 通过禁止将trule作为左值的方法，因为左值允许取址和赋值操作，这种特性容易导致其用于其他地方而没有报错。
48	Trule(Trule<T>&);
49	Trule<T>& operator= (Trule<T>&); // 私有声明禁止拷贝赋值
50	friend class Holder<T>;
51	};

需要注意的是，上面的代码并不完全是把一个holder完全转换为一个trule：如果是这样的话，holder就必须是一个可修改的左值。这也是我们为什么要使用一个单独的类型来实现trule，而不是将它的功能合并到holder类模板中的原因。

最后，对于上面实现的trule，只有被holder模板所辨识并且使用之后，才能算是完整的。如下：

template <typename T>
class Holder
{
    // 前面已经定义的成员
    ...

    public:
        Holder(Trule<T> const& t){
            ptr = t.ptr;
            const_cast<Trule<T>&>(t).ptr = 0;
        }

        Holder<T>& operator= (Trule<T> const& t) {
            delete ptr;
            ptr = t.ptr;
            const_cast<Trule<T>&>(t).ptr = 0;
            return *this;
        }
};

为了充分演示对holder/trule作了哪些改善，我们可以重写load_something()例子，如下：

#include "holder2.hpp"
#include "trule.hpp"

class Something
{
};

void read_something(Something* x)
{
}

// 返回类型为Trule<Something>，通过将Holder<Something>转换成返回类型(也即，通过trule传递返回值)
Trule<Something> load_something()
{
    Holder<Something> result(new Something);
    read_something(result.get());
    return result;
}

int main()
{
    // 接收load_something函数返回的Trule<Something>类型的值，并通过Holder内部接收Trule对象的构造函数初始化Holder对象ptr
    Holder<Something> ptr(load_something());
    ....
}

引用计数

设计一个引用计数的智能指针，基本思想是：对于每个被指向的对象，都保存一个计数，用于代表指向该对象的指针的个数，当计数值减少到0时，就删除此对象。

我们首先面对的问题是：计算器在什么地方？这里可以有两种方式，一种是把计算器放在对象中，但如果对象早期已经设计好，则无法再把计算器放入对象；另一种也是通常会使用的就是使用专用的（内存）分配器。

我们面对的第二个问题是：对象的析构和释放。我们有可能会需要使用非标准方式（比如C的free()，或者delete[]运算符释放对象数组）来释放对象，故而，我们还需要指定一种单独的对象（释放）policy。

对于大多数用CountingPtr计数的对象，我们可以使用下面这个简单的对象policy：

// pointers/stdobjpolicy.hpp
class StandardObjectPolicy
{
    public:
        template<typename T> void dispose(T* object){
            delete object;
        }
};

// pointers/stdarraypolicy.hpp
class StandardArrayPolicy
{
    public:
        template<typename T> void dispose(T* array){
            delete[] array;
        }
};

在考虑了上面两个问题之后，我们现在开始定义我们的CountingPtr模板：

/* pointers/countingptr.hpp */

template <typename T,
	  typename CounterPolicy	= SimpleReferenceCount,         /* 计算器的policy */
	  typename ObjectPolicy		= StandardObjectPolicy>         /* 对象（释放）policy */

class CountingPrt : private CounterPolicy, private ObjectPolicy
{
private:
	/* typedef 两个简单的别名 */
	typedef CountPolicy	CP;
	typedef ObjectPolicy	OP;

	T* object_pointer_to;         /* 所引用的对象 */
	/* 如果没有引用任何对象，则为NULL */

public:
	/* 缺省构造函数（没有显式初始化，即没有加上explicit关键字） */
	CountingPtr()
	{
		this->object_pointed_to = NULL;
	}

	/* 一个针对转型的构造函数（转型自一个内建的指针） */
	explicit CountingPtr( T* p )
	{
		this->init( p );        /* 使用普通指针初始化 */
	}

	/* 拷贝构造函数 */
	CountingPtr( CountingPtr<T, CP, OP> const & cp )
		: CP( (CP const &)cp ), /* 拷贝policy */
		OP( (OP const &)cp )
	{
		this->attach( cp );     /* 拷贝指针，并增加计数值 */
	}

	/* 析构函数 */
	~CountingPtr()
	{
		this->detach();         /* 减少计数值，如果计数值为0，则释放该计数器 */
	}

	/* 针对内建指针的赋值运算符 */
	CountingPtr<T, CP, OP> & operator=( T* p )
	{
		/* 计数指针不能指向*p */
		assert( p != this->object_pointed_to );
		this->detach();         /* 减少计数值，如果计数值为0，则释放该计数器 */

		this->init( p );        /* 用一个普通指针进行初始化 */
		return(*this);
	}

	/* 拷贝赋值运算符（要考虑自己给自己赋值） */
	CountingPtr<T, CP, OP> &
	operator=( CountingPtr<T, CP, OP> const & cp )
	{
		if ( this->object_pointed_to != cp.object_pointed_to )
		{
			this->detach();                         /* 减少计数值，如果计数值为0，则释放该计数器 */

			CP::operator=( (CP const &)cp );        /* 对policy进行赋值 */
			OP::operator=( (OP const &)op );
			this->attach( cp );                     /* 拷贝指针并增加计数值 */
		}
		return *this ；
	}

	/* 使之成为智能指针的运算符 */
	T* operator->() const
	{
		return(this->object_pointed_to);
	}

	T & operator*() const
	{
		return(*this->object_pointed_to);
	}

	/* 以后在这里将可能会增加一些其他的接口 */
	....

private:
	/*
	 * 辅助函数
	 * - 用普通指针进行初始化（前提是普通指针存在）
	 */
	void init( T* p )
	{
		if ( p != NULL )
		{
			CounterPolicy::init( p );
		}
		this->object_pointed_to = p;
	}

	/* - 拷贝指针并且增加计数值（前提是指针存在） */
	void attach( CountingPtr<T, CP, OP> const & cp )
	{
		this->object_pointed_to = cp.object_pointed_to;
		if ( cp.object_pointed_to != NULL )
		{
			CounterPolicy::increment( cp.object_pointed_to );
		}
	}

	/* - 减少计数值（如果计数值为0， 则释放计数器） */
	void detach()
	{
		if ( this->object_pointed_to != NULL )
		{
			CounterPolicy::decrement( this->object_pointed_to );
			if ( CounterPolicy::is_zero( this->object_pointed_to ) )
			{
				/* 如果有必要的话，释放计数器 */
				CounterPolicy::dispose( this->object_pointed_to );
				/* 使用object policy来释放所指向的对象 */
				ObjectPolicy::dispose( this->object_pointed_to );
			}
		}
	}
};

上面代码需要注意：

在拷贝赋值操作中，要判断是否为自赋值；
由于空指针并没有一个可关联的计数器，所以在减少计数值之前，必须先显式地检查空指针的情况；
在前面的代码中，我们使用继承来包含两种policy。这样做确保了在policy类为空的情况下，并不需要占用存储空间（前提是我们的编译器实现了空基类优化）

一个简单的非侵入式计数器

从总体看来，我们已经完成了CountingPtr的设计，下面我们需要为计数policy编写代码。

于是，我们先来看一个针对计数器的policy，它并不把计数器存储于所指向对象的内部，也就是说，它是一种非侵入式的计数器policy（或者称为非插入式的计数器policy）。

对于计数器而言，最主要的问题是如何分配存储空间。事实上，同一个计数器需要被多个CountingPtr所共享；因此，它的生命周期必须持续到最后一个智能指针被释放之后。

通常而言，我们会使用一种特殊的分配器来完成这种任务，这种分配器专门用于分配大小固定的小对象。

// pointers/simplerefcount.hpp

#include <stddef.h> // 用于size_t的定义
#include "allocator.hpp"

class SimpleReferenceCount
{
    private:
        size_t* counter;        // 已经分配的计数器
    public:
        SimpleReferenceCount(){
            counter = NULL;
        }

        // 缺省的拷贝构造函数和拷贝赋值运算符都是允许的
        // 因为它们只是拷贝这个共享的计数器
    public:
        // 分配计数器，并把它的值初始为1
        template <typename T> void init(T*) {
            Counter = alloc_counter();
            *counter = 1;
        }

        // 释放该计数器
        template <typename T> void dispose(T*) {
            dealloc_counter(counter);
        }

        // 计数值加1
        template<typename T> void increment(T*){
            ++*counter;
        }

        // 计数值减1
        template<typename T> void decrement(T*){
            --*counter;
        }

        // 检查计数值是否为0
        template<typename T> bool is_zero(T*){
            return *counter == 0;
        }
};

一个简单的侵入式计数器模板

侵入式（或插入式）计数器policy就是将计数器放到被管理对象本身的类型中（或者可能存放到由被管理对象所控制的存储空间中）。显然，这种policy通常需要在设计对象类型的时候就加以考虑；因此这种方案很可能会专用于被管理对象的类型。

// pointers/memberrefcount.hpp

template<typename ObjectT,        // 包含计数器的类型
            typename CountT,             // 计数器的类型
            CountT Object::*CountP>   // 计数器的位置，在设计ObjectT对象的时候就考虑到计数器
class MemberReferenceCount
{
    public:
        // 缺省构造函数和析构函数都是允许的

        // 让计数器的值初始化为1
        void init(ObjectT* object){
            object->*CountP = 1;
        }

        // 对于计数器的释放，并不需要显式执行任何操作
        void dispose(ObjectT*){ }

        // 计数器加1
        void increment(ObjectT* object){
            ++object->*CountP;
        }

        // 计数器减1
        void increment(ObjectT* object){
            --object->*CountP;
        }

        // 检查计数值是否为0
        template<typename T> bool is_zero(ObjectT* object){
            return object->*CounP == 0;
        }
};

如果使用这种policy的话，那么在类的实现中，就可以很快地写出类的引用计数指针类型。其中类的设计框架大概如下：

class ManagedType
{
    private:
        size_t ref_count;
    public:
        typedef CountingPtr<ManagedType,
                                       MemberReferenceCount
                                      <ManagedType,        // 包含计数器的对象类型
                                        size_t,                   // 计数器类型
                                        &ManagedType::ref_count>>
                    Ptr;
        ....
};

有了上面这个定义之后，我们就可以使用ManageeType::Ptr方便地引用“那些用于访问ManagedType对象的”引用计数指针类型（在此为智能指针类型CountingPtr）。
C++ Template By David Vandevoorde还介绍了关于智能指针的其他一些功能实现，包括常数性相关内容、隐式转型，以及比较等等，有兴趣自行查阅学习，这里不介绍

tuple

duo

自定义的duo的目的是把两个对象聚集到一个单一类型（类似标准库的std::pair）。

1	template <typename T1, typename T2>
2	struct Duo
3	{
4	//add2: 提供域类型的访问
5	typedef T1 Type1; // 第1个域的类型
6	typedef T2 Type2; // 第2个域的类型
7	enum { N = 2 }; // 域的个数
8	// end add2
9
10	T1 v1; // 第1个域的值
11	T2 v2; // 第2个域的值
12
13	//add1: 并且给它添加两个构造函数
14	Duo() : v1(), v2() { }
15	Duo(T1 const&a, T2 const& b) : v1(a), v2(b) { }
16	// end add1
17	};
18
19	// 辅助函数
20	template <typename T1, typename T2>
21	inline
22	Duo<T1, T2> make_duo(T1 const& a, T2 const& b)
23	{
24	return Duo<T1, T2>(a, b);
25	}
26
27	// 对于某些需要判断返回结果是否有效的函数而言会很有用
28	Duo<bool, X> result = foo();
29	if (result.v1)
30	{
31	// 结果是有效的，返回值是result.v2
32	...
33	}
34
35	// 创建和初始化Duo也非常简单
36	make_duo(true, 42);

上面实现的duo已经很接近std::pair了，但还有一些不同之处，如在构造函数中我们没有提供用于隐式类型转换的成员模板初始化函数；没有提供比较运算符等；基于这些区别，我们下面给出一个更强大清晰的实现：

// tuples/duo1.hpp

#ifndef DUO_HPP
#define DUO_HPP

template <typename T1, typename T2>
class Duo
{
    public:
        // 提供域类型的访问
        typedef T1 Type1;             // 第1个域的类型
        typedef T2 Type2;             // 第2个域的类型
        enum { N = 2 };                    // 域的个数

    private:
        T1 value1;       // 第1个域的值
        T2 value2;       // 第2个域的值

    public:
        // 并且给它添加两个构造函数
        Duo() : value1(), value2() { }
        Duo(T1 const&a, T2 const& b) : value1(a), value2(b) { }

        // 用于在构造期间，进行隐式的类型转换
        template <typename U1, typename U2>
        Duo(Duo<U1, U2> const& d)
            : value1(d.v1()), value2(d.v2()) { }

        // 用于在赋值期间，进行隐式的类型转换
        template<typename U1, typename U2>
        Duo<T1, T2>& operator= (Duo<U1, U2> const& d){
            value1 = d.value1;
            value2 = d.value2;
            return *this;
        }

        // 用于访问域的函数（域访问函数）
        T1& v1(){
            return value1;
        }

        T1 const& v1() const {
            return value1;
        }

        T2& v2(){
            return value2;
        }

        T2 const& v2() const {
            return value2;
        }
};

// 比较运算符（允许混合类型）：
template<typename T1, typename T2, typename U1, typename U2>
inline 
bool operator==(Duo<T1, T2> const& d1, Duo<U1, U2> const& d2)
{
    return d1.v1() == d2.v1() && d1.v2() == d2.v2();
}

template<typename T1, typename T2, typename U1, typename U2>
inline 
bool operator!=(Duo<T1, T2> const& d1, Duo<U1, U2> const& d2)
{
    return !(d1 == d2);
}

// 针对创建和初始化的辅助函数
template<typename T1, typename T2>
inline
Duo<T1, T2> make_duo(T1 const& a, T2 const& b)
{
    return Duo<T1, T2>(a, b);
}

#endif // DUO_HPP

// tuples/duo1.cpp
#include "duo1.hpp"
Duo<float, int> foo()
{
    // Duo<int, int> 到返回类型Duo<float, int>的隐式转型
    return make_duo(42, 42);
}

int main()
{
    // Duo<float, int> 到返回类型Duo<int, double>的隐式转型
    if (foo() == make_duo(42, 42.0))
    {
        ...
    }
}

可递归duo

域的个数

// tuples/duo2.hpp
template <typename A, typename B, typename C>
class Duo<A, Duo<B, C> >
{
    public:
        typedef A            T1;       // 第1个域的类型
        typedef Duo<B, C>            T2;       // 第2个域的类型
        enum { N = Duo<B, C>::N + 1 };            // 域的个数

    private:
        T1 value1;                // 第1个域的值
        T2 value2;                // 第2个域的值

    public:
        // 其他的公共成员都不需要改变
        .....
};

// tuples/duo6.hpp
// 相应的递归出口
template <typename A>
struct Duo<A, void>
{
    public:
        typedef A        T1;          // 第1个域的类型
        typedef void        T2;          // 第2个域的类型
        enum { N = 1 };            // 域的个数

    private:
        T1 value1;                // 第1个域的值

    public:
        // 构造函数
        Duo() : value1() {}
        Duo(T1 const& a) : value1(a) {}

        // 域访问函数
        T1& v1(){
            return value1;
        }

        T1 const& v1() const{
            return value1;
        }

        void v2() {}
        void v2() const{}
        ....
};

域的类型
用于获取duo的第N个域的类型（即T）的基本模板

// （1）对于non-Duo（非duo）而言，结果类型为void
template <int N, typename T>
class DuoT
{
    public:
        typedef void ResultT;         // 一般情况下，结构类型是void
};

// （2）对于非递归的duo，定义两个简单的局部特化，用于获取每个域的类型
// 针对普通duo第1个域的特化
template <typename A, typename B>
class DuoT<1, Duo<A, B> >
{
    public:
        typedef A ResultT;
};

// 针对普通duo第2个域的特化
template <typename A, typename B>
class DuoT<2, Duo<A, B> >
{
    public:
        typedef B ResultT;
};

// （3）可递归duo的第N个域的类型：一般情况下，它等于第2个域的第N-1个域的类型
// 针对可递归duo第N个域的类型的特化
template <int N, typename A, typename B, typename C>
class DuoT<N, Duo<A, Duo<B, C> > >
{
    public:
        typedef typename DuoT<N-1, Duo<B, C> >::ResultT ResultT;
};

// （4）另外，针对可递归duo第1个（域的）类型的特化如下
// 针对可递归duo第1个域的特化
template <typename A, typename B, typename C>
class DuoT<1, Duo<A, Duo<B, C> > >
{
    public:
        typedef A ResultT;
};

// 针对可递归duo第2个（域的）类型的特化如下
// 针对可递归duo第2个域的特化
template <typename A, typename B, typename C>
class DuoT<2, Duo<A, Duo<B, C> > >
{
    public:
        typedef B ResultT;
};

域的值
在一个可递归duo中，就操作而言，抽取第N个值与抽取第N个类型是类似的，只是抽取第N个值要稍微复杂一些。为了能够抽取第N个值，我们需要实现一个形为val(duo)的接口。但是在实现该接口的过程中，我们需要先实现一个辅助类模板DuoValue，因为只有类模板才能够被局部特化（函数模板现在还不可以），而局部特化能够帮助我们高效地抽取第N个值。如下：

#include "typeop.hpp"

// 返回变量duo的第N个值
template <int N, typename A, typename B>
inline
typename TypeOp<typename DuoT<N, Duo<A, B> >::ResultT>::RefT
val(Duo<A, B>& d)
{
    return DuoValue<N, Duo<A, B> >::get(d);
}

// 返回常量duo的第N个值
template <int N, typename A, typename B>
inline
typename TypeOp<typename DuoT<N, Duo<A, B> >::ResultT>::RefConstT
val(Duo<A, B> const& d)
{
    return DuoValue<N, Duo<A, B> >::get(d);
}

总结

下面是DuoValue的一个完整实现

#include "typeop.hpp"

//基本模板，针对（duo）T的第N个值
template <int N, typename N>
class DuoValue
{
    public:
        static void get(T&) { }        // 一般情况下，并不返回值
        static void get(T const&) { }
};

// 针对普通duo的第N个域的特化
template <int N, typename N>
class DuoValue<1, Duo<A, B> >
{
    public:
        static A& get(Duo<A, B> & d) {
            return d.v1();
        }
        static A const& get(Duo<A, B> const&) {
            return d.v1();
        }
};

// 针对普通duo第2个域的特化
template <typename A, typename B>
class DuoValue<2, Duo<A, B> >
{
    public:
        static B& get(Duo<A, B> &d){
            return d.v2();
        }

        static B const& get(Duo<A, B> const &d){
            return d.v2();
        }
};

// 针对可递归duo的第N个值的特化
template <int N, typename A, typename B, typename C>
struct DuoValue<N, Duo<A, Duo<B, C> > >
{
    static
    typename TypeOp<typename DuoT<N-1, Duo<B, C> >::ResultT>::RefT
    get(Duo<A, Duo<B, C> > &d){
        return DuoValue<N-1, Duo<B, C> >::get(d.v2());
    }

    static typename TypeOp<typename DuoT<N-1, Duo<B, C>
                                    >::ResultT>::RefConstT
    get(Duo<A, Duo<B, C> > const &d){
        return DuoValue<N-1, Duo<B, C> >::get(d.v2());
    }
};

// 针对可递归duo的第1个域的特化
template <typename A, typename B, typename C>
class DuoValue<1, Duo<A, Duo<B, C> >
{
    public:
        static A& get(Duo<A, Duo<B, C> > &d){
            return d.v1();
        }

        static A const& get(Duo<A, Duo<B, C> > const &d){
            return d.v1();
        }
};

// 针对可递归duo的第2个域的特化
template <typename A, typename B, typename C>
class DuoValue<2, Duo<A, Duo<B, C> > >
{
    public:
        static B& get(Duo<A, Duo<B, C> > &d){
            return d.v2().v1();
        }

        static B const& get(Duo<A, Duo<B, C> > const &d){
            return d.v2().v1();
        }
};

下面程序给出如何使用上面的duo：

1	// 创建和使用一个简单的duo
2	Duo<bool, int> d;
3	std::cout << d.v1() << std::endl;
4	std::cout << val<1>(d) << std::endl;
5
6	// 创建和使用triple
7	Duo<bool, Duo<int, float> > t;
8
9	val<1>(t) = true;
10	val<2>(t) = 42;
11	val<3>(t) = 0.2;
12
13	std::cout << val<1>(t) << std::endl;
14	std::cout << val<2>(t) << std::endl;
15	std::cout << val<3>(t) << std::endl;

例如,调用

val<3>(t)

最后将会扩展为

1	t.v2().v2()

tuple构造

上一节我们了解到可递归duo的嵌套结构有助于展现metaprogramming技术的应用，现在我们为把该结构封装成一个简单接口，从而可以在日常工作中使用这种结构。为了实现这种接口，我们可以定义一个含有多个参数的可递归tuple模板，并让它派生自一个可递归duo类型，其中该duo类型的域个数是有限制的（假设最多5个域）。

为了使tuple的大小（即域个数）是可变的，我们声明了一些无用的类型参数，它们缺省值是一个null类型；在此，我们特地定义了一个NullT类型，用于代表这种null类型。之所以使用NullT，而不使用void，是因为我们需要创建该类型（即NullT）的参数，而void是不能作为参数类型的：

1	// 用于代表无用类型参数的类型
2	class NullT
3	{
4	};

接下来，我们把tuple定义为一个模板，它派生自duo，而且该duo至少具有一个定义为NullT的类型参数：

// 一般情况下，Tuple<>都创建自“至少含有一个NullT的另一个Tuple<>”
template <typename P1,
                typename P2 = NullT,
                typename P3 = NullT,
                typename P4 = NullT,
                typename P5 = NullT>
class Tuple
    : public Duo<P1, typename Tuple<P2, P3, P4, P5, NullT>::BaseT>
{
    public:
        typedef Duo<P1, typename Tuple<P2, P3, P4, P5, NullT>::BaseT> BaseT;

        // 构造函数
        Tuple() { }
        Tuple(TypeOp<P1>::RefConstT a1,
                Tuple(TypeOp<P2>::RefConstT a2,
                Tuple(TypeOp<P3>::RefConstT a3 = NullT(),
                Tuple(TypeOp<P4>::RefConstT a4 = NullT(),
                Tuple(TypeOp<P5>::RefConstT a5 = NullT())
            : BaseT(a1, Tuple<P2, P3, P4, P5, NullT>(a2, a3, a4, a5)){   // 递归减少参数个数
        }
};

// 用于终止递归的特化
template <typename P1, typename P2>
class Tuple<P1, P2, NullT, NullT, NullT> : public Duo<P1, P2>
{
    public:
        typedef Duo<P1, P2> BaseT;
        Tuple() { }

        Tuple(TypeOp<P1>::RefConstT a1,
                Tuple(TypeOp<P2>::RefConstT a2,
                Tuple(TypeOp<NullT>::RefConstT = NullT(),
                Tuple(TypeOp<NullT>::RefConstT = NullT(),
                Tuple(TypeOp<NullT>::RefConstT = NullT())
            : BaseT(a1, a2){
        }
};

于是，有一个如下的声明：

1	Tuple<bool, int, float, double> t4(true, 42, 13, 1.95583);

而其他的特化将会考虑tuple是一个singleton（即只具有一个域）的情形：

// 针对singletons的特化
template <typename P1>
class Tuple<P1, NullT, NullT, NullT, NullT> : public Duo<P1, void>
{
    public:
        typedef Duo<P1, void> BaseT;
        Tuple() { }

        Tuple(TypeOp<P1>::RefConstT a1,
                Tuple(TypeOp<NullT>::RefConstT = NullT(),
                Tuple(TypeOp<NullT>::RefConstT = NullT(),
                Tuple(TypeOp<NullT>::RefConstT = NullT(),
                Tuple(TypeOp<NullT>::RefConstT = NullT())
            : BaseT(a1){
        }
};

最后，我们定义类似make_duo()的辅助函数，对每种不同大小的tuple，都需要声明一个不同的函数模板make_duo()，因为函数模板不能含有缺省模板实参，而且在模板参数的演绎过程中，也不会考虑缺省的函数调用实参：

// 针对一个实参的辅助函数
template <typename T1>
inline
Tuple<T1> make_duo(T1 const& a1)
{
    return Tuple<T1>(a1);
}

// 针对两个实参的辅助函数
template <typename T1, typename T2>
inline
Tuple<T1, T2> make_duo(T1 const& a1, T2 const& a2)
{
    return Tuple<T1, T2>(a1, a2);
}

// 针对3个实参的辅助函数
template <typename T1, typename T2, typename T3>
inline
Tuple<T1, T2, T3> make_duo(T1 const& a1, T2 const& a2, T3 const& a3)
{
    return Tuple<T1, T2, T3>(a1, a2, a3);
}

// 针对4个实参的辅助函数
template <typename T1, typename T2, typename T3, typename T4>
inline
Tuple<T1, T2, T3, T4> make_duo(T1 const& a1, T2 const& a2, T3 const& a3, T4 const& a4)
{
    return Tuple<T1, T2, T3, T4>(a1, a2, a3, a4);
}

// 针对5个实参的辅助函数
template <typename T1, typename T2, typename T3, typename T4, typename T5>
inline
Tuple<T1, T2, T3, T4, T5> make_duo(T1 const& a1, T2 const& a2, T3 const& a3, T4 const& a4, T5 const& a5)
{
    return Tuple<T1, T2, T3, T4, T5>(a1, a2, a3, a4, a5);
}

如何使用该tuple：

1	// 创建和使用只具有1个域的tuple
2	Tuple<int> t1;
3	val<1>(t1) += 42;
4	std::cout << t1.v1() << std::endl;
5
6	// 创建和使用duo
7	Tuple<bool, int> 42;
8	std::cout << val<1>(t2) << ", " ;
9	std::cout << t2.v1() << std::endl;
10
11	// 创建和使用triple
12	Tuple<bool, int, double> t3;
13
14	val<1>(t3) = true;
15	val<2>(t3) = 42;
16	val<3>(t3) = 0.2;
17
18	std::cout << val<1>(t3) << ", ";
19	std::cout << val<2>(t3) << ", ";
20	std::cout << val<3>(t3) << std::endl;
21
22	t3 = make_tuple(false, 23, 13.13);
23	std::cout << val<1>(t3) << ", ";
24	std::cout << val<2>(t3) << ", ";
25	std::cout << val<3>(t3) << std::endl;
26
27	// 创建和使用quadruple
28	Tuple<bool, int, float, double> t4(true, 42, 13, 1.95583);
29	std::cout << val<4>(t4) << std::endl;
30	std::cout << t4.v2().v2().v2() << std::endl;

函数对象和回调

函数对象（也称为__仿函数__）是指：可以使用函数调用语法进行调用的任何对象。

在C程序设计语言中，有3种类似于函数调用语法的实体：函数、类似于函数的宏和函数指针。由于函数和宏实际上并不是对象，因此在C语言中，我们只把函数指针看成仿函数。

然而在C++中，还存在其他的函数对象：对于class类型，我们可以重载函数调用运算符；还存在函数引用的概念；另外，成员函数和成员函数指针也都有自身的调用语法。

本节在于把仿函数的概念和模板所提供的编译期参数化机制结合起来以提供更加强大的程序设计技术。

仿函数的习惯用法几乎都是使用某种形式的回调，而回调的含义是这样的：对于一个程序库，它的客户端希望该程序库能够调用客户端自定义的某些函数，我们就把这种调用称为回调。

直接调用、间接调用和内联调用

在阐述如何使用模板来实现有用的仿函数之前，我们先讨论函数调用的一些属性，也正是这些属性的差异，才真正体现出基于模板的仿函数的优点。

使用内联的优点：在一个调用系列中，不但能够避免执行这些（查找名称的）机器代码；而且能够让优化器看到函数对传递进来的变量进行了哪些操作。

实际上，我们在后面将会看到，如果我们使用基于模板的回调来生成机器码的话，那么这些机器码将主要涉及到直接调用和内联调用；而如果用传统的回调的话，那么将会导致间接调用。使用模板的回调将会大大节省程序的运行时间。

函数指针与函数引用

考虑函数foo()定义：

1	extern "C++" void foo() throw()
2	{
3	}

该函数的类型为：具有C链接的函数，不接受参数，不返回值并且不抛出异常。由于历史原因，在C语言的正式定义中，并没有把异常规范并入函数类型的一部分。然而，将来的标准将会把异常加入函数类型中。
实际上，当你自己编写的代码要和某个函数进行匹配时，通常也应该要求异常规范同时也是匹配的。名字链接（通常只存在于C和C中）是类型系统的一部分，但某些C编译器将会自动添加这种链接。特别地，这些编译器允许具有C链接的函数指针和具有C链接的函数指针相互赋值。这同时带来下面的一个事实：在大多数平台上，C和C函数的调用规范几乎是一样的，唯一的区别在于：C++将会考虑参数的类型和返回值的类型。

在大多数上下文中，表达式foo能够转型为指向函数foo()的指针。即使foo本身并没有指针的含义，但是就如表达式ia一样，在声明了下面的语句之后：

1	int ia[10];

ia将隐含地表示一个数组指针（或者是一个指向数组第1个元素的指针）。于是，这种从函数（或者数组）到指针的转型通常也被称为decay。如下：

1	// functors/funcptr.cpp
2
3	#include <iostream>
4	#include <typeinfo>
5
6	void foo()
7	{
8	std::cout << "foo() called" << std::endl;
9	}
10
11	typedef void FooT(); // FooT是一个函数类型，与函数foo()具有相同的类型
12
13	int main()
14	{
15	foo(); // 直接调用
16
17	// 输出foo和FooT的类型
18	std::cout << "Types of foo: " << typeid(foo).name() << '\n';
19	std::cout << "Types of FooT: " << typeid(FooT).name() << '\n';
20
21	FooT* pf = foo; // 隐式转型（decay）
22	pf(); // 通过指针的间接调用
23	(*pf)(); // 等价于pf()
24
25	// 打印出pf的类型
26	std::cout << "Types of pf : " << typeif(pf).name() << '\n';
27
28	FooT& rf = foo; // 没有隐式转型
29	rf(); // 通过引用的间接调用
30
31	// 输出rf的类型
32	std::cout << "Types of rf : " << typeid(rf).name() << '\n';
33	}
34	//-----------------------------------------------
35	输出：
36	foo() called
37	Types of foo: void()
38	Types of FooT: void()
39	foo() called
40	foo() called
41	Types of pf: FooT * // 输出类型不是void()而是FooT
42	foo() called
43	Types of rf: void ()

该例子同时也说明了：作为语言的一个概念，函数引用（或者称为指向函数的引用）是存在的；但是我们通常都是使用函数指针（而且为了避免产生混淆，最后还是继续使用函数指针）。另外，表达式foo实际上是一个左值，因为它可以被绑定到一个non-const类型的引用；然而，我们却不能修改这个左值。

我们另外还发现：在函数调用中，可以使用函数指针的名称（如pf）或者函数引用的名称（如rf）来进行函数调用，就像所有函数名称本身一样。

因此，可以认为一个函数指针本身就是一个仿函数——一个在函数调用语法中可以用于代替函数名称的对象。另一方面，由于引用并不是一个对象，所有函数引用并不是仿函数。最后，如果基于我们前面所讨论的直接调用和间接调用来看，那么这些看起来相同的符号却很可能会有很大的性能差距。

成员函数指针

典型的C++实现（也即编译器）是如何处理成员函数调用的？首先考虑下面的程序：

1	class B1
2	{
3	private:
4	int b1;
5	public:
6	void mf1();
7	};
8	void B1::mf1()
9	{
10	std::cout << "b1 = " << b1 << std::endl;
11	}
12	//--------------------------------
13	class B2
14	{
15	private:
16	int b2;
17	public:
18	void mf2();
19	};
20	void B2::mf2()
21	{
22	std::cout << "b2 = " << b2 << std::endl;
23	}
24	//--------------------------------
25	class D : public B1, public B2
26	{
27	private:
28	int d;
29	};

对成员函数mf1或mf2调用语法p->mf_x()，p会是一个指向对象或子对象的指针，以某种隐藏参数的形式传递给mf_x，大多是作为this指针的形式传递。

有了上面这个定义之后，D类型对象不但具有B1类型对象的行为，同时也具有B2类型对象的行为。为了实现D类型对象的这种特性，一个D对象就需要既包含一个B1对象，也包含一个B2对象。

在我们今天所指定的几乎所有的32位编译器中，如果int成员占用4个字节的话，那么成员b1的地址为this的地址，成员b2的地址为this地址再加上4个字节，而成员d的地址为this地址加上8个字节。B1和B2最大的区别在于：B1的子对象（即b1）与D的子对象共享起始地址（即this地址），而B2的子对象（即b2）则没有。

现在，考虑使用成员函数指针进行函数调用：

void call_memfun (D obj, void(D::*pmf) () )
{
    (obj.*pmf) ();
}

int main()
{
    D obj;
    call_memfun(obj, &D::mf1);
    call_memfun(obj, &D::mf2);
}

从上面调用代码我们得出一个结论：对于某些成员函数指针，除了需要指定函数的地址之外，还需要知道基于this指针的地址调整。如果在考虑到虚函数的时候又会有其他的许多不同。编译器通常使用3-值结构：

成员函数的地址，如果是一个虚函数的话，那么该值为NULL；
基于this的地址调整；
一个虚函数索引。

成员变量指针实际上并不是一个真正意义上的指针，而是一些基于this指针的偏移量，然后根据this指针和对应的偏移量，才能获取给定的域（即成员变量的值，对于值域而言，在内存中可以表示为一块固有的存储空间）。

对于通过成员函数指针访问成员函数的操作，实际上是一个2元操作，因为它不仅仅需要知道对应的成员函数指针（即下面的pmf），还需要知道包含该成员函数的对象（即下面的obj）。于是，在语言中引入特殊的成员指针取引用运算符.和->：

1	(obj.*pmf)(...) // 调用位于obj中的、pmf所引用的成员函数
2	(ptr->*pmf)(...) // 调用位于ptr所引用对象中的、pmf所引用的成员函数

相对而言，通过指针访问一个普通函数就是一个一元操作：

(*ptr)()

从前面我们知道，上面这个解引用运算符可以省略不写，因为在函数调用运算符中，解引用运算符是隐式存在的。因此，前面的表达式通常可以写出：

ptr()

但是对于__函数指针而言，却不存在这种隐式（存在）的形式__。

对于成员函数名称而言，同样不存在隐式的decay，例如MyType::print不能隐式decay为对应的指针形式（即&MyType::print），其中这个&号是必须写的，并不能省略。然而对于普通函数而言，把f隐式decay为&f是很常见的，也是众所周知的。

class类型的仿函数

在C++语言中，虽然函数指针直接就是现成的仿函数；然而，在很多情况下，如果使用重载了函数调用运算符的class类型对象的话，可以给我们带来很多好处：譬如灵活性、性能，甚至二者兼备。
下面是class类型仿函数的一个简单例子：

#include <iostream>

// 含有返回常值的函数对象的类
class ConstantIntFunctor
{
    private:
        int value;    // “函数调用”所返回的值
    public:
        // 构造函数：初始化返回值
        ConstantIntFunctor (int c) : value(c) {}

        // “函数调用”
        int operator() () const {
            return value;
        }
};

// 使用上面“函数对象”的客户端函数
void client (ConstantIntFunctor const& cif)
{
    std::cout << "calling back functor yields " << cif() << '\n' ;
}

int main()
{
    ConstantIntFunctor seven(7);
    ConstantIntFunctor fortytwo(42);
    client(seven);
    client(fortytwo);
}

ConstantIntFunctor是一个class类型，而它的仿函数就是根据该类型创建出来的。也就是说，如果你使用下面语句生成一个对象：

1	ConstantIntFunctor seven(7); // 生成一个名叫seven的函数对象

那么表达式：

1	seven(); // 调用函数对象的operator()

就是调用对象seven的operator()，而不是调用函数seven()。实际上，我们传递函数对象seven和fortytwo给client()的参数cif，（间接地）获得了和传递函数指针完全一样的效果。

该例如同时也说明了：在实际应用中，class类型仿函数的优点所在（与函数指针相比）：能够在函数中关联某些状态（也即成员变量），这可能也是class类型仿函数最重要的优点。而对于回调机制而言，这种优点能够带来功能上的提升。因为对于一个函数而言，我们现在能够根据不同的参数（主要指成员变量）来生成不同的函数实例（如前面的seven和fortytwo）。

class类型仿函数的类型

与函数指针相比，class类型仿函数除了具有状态信息之外，还具有其他的特性。实际上，如果一个class类型仿函数并没有包含任何状态的话，那么它的行为完全是由它的类型所决定的。于是，我们可以以模板实参的形式来传递该类型，用于自定义程序库组件的行为。

对于上面的这种实现，一个经典的例子是：以某种顺序对它的元素进行排序的容器类，其中排序规则就是一个模板实参。另外，由于排序规则是容器类型的一部分，所以如果对某个特定容器混合使用多种不同的排序规则（例如在赋值运算符中，两个容器使用不同的排序规则，就不能相互赋值），类型系统通常都会给出错误。

作为模板类型实参的仿函数

传递仿函数的一个方法是让它的类型作为一个模板实参。然而类型本身并不是一个仿函数，因此客户端函数或者客户端类必须创建一个给定类型的仿函数对象。当然，只有class类型仿函数才能这么做，函数指针则不可以；而且函数指针本身也不会指定任何行为。另外，也不存在一种能够传递包含状态的类型的机制（因为类型本身并不包含任何特定的状态，只有对象才可能具有某些特定的状态，所以在此真正要传递的是一个特定的对象）。

下面是函数模板的一个雏形，它接收一个class类型的仿函数作为排序规则：

1	template <typename FO>
2	void my_sort(... )
3	{
4	FO cmp; // 创建函数对象
5	...
6	if (cmp(x, y)) // 使用函数对象来比较2个值
7	{
8	....
9	}
10	....
11	}
12	// 以仿函数为模板实参，来调用函数
13	my_sort<std::less<... > > (... );

运用上面这个方法，比较代码（如std::less<>）的选择将会是在编译期进行的。并且由于比较操作是内联的，所以一个优化的编译器将能够产生本质上等价于不使用仿函数，而直接编写的代码。

作为函数调用实参的仿函数

另一种传递仿函数的方法是以函数调用实参的形式进行传递。这就允许调用者在运行期构造函数对象（可能使用一个非虚拟的构造函数）

就作用而言，函数调用实参和函数类型参数本质上是类似的，唯一的区别在于：当传递参数的时候，函数调用实参需要拷贝一个仿函数对象。这种拷贝开销通常是很低的，而且实际上如果该仿函数对象没有成员变量的话（而实际情况也经常如此），那么这种拷贝开销也将接近于0。如下：

1	template <typename F>
2	void my_sort(... , F cmp)
3	{
4	...
5	if (cmp(x, y)) // 使用函数对象，来比较两个值
6	{
7	...
8	}
9	...
10	}
11	// 以仿函数作为调用实参，调用排序函数
12	my_sort(... , std::less<... >());

结合函数调用参数和模板类型参数

对于前面两种传递仿函数的方式——即传递函数指针和class类型的仿函数，只要通过定义缺省函数调用实参，是完全可以把这两种方式结合起来的：

1	template <typename F>
2	void my_sort(... , F cmp = F() )
3	{
4	...
5	if (cmp(x, y)) // 使用函数对象来比较两个值
6	{
7	...
8	}
9	...
10	}
11	bool my_criterion() (T const& x, T const& y);
12	// 借助于模板实参传递进来的仿函数，来调用排序函数
13	my_sort<std::less<... > > (... );
14
15	// 借助于值实参（即函数实参）传递进来的仿函数，来定义排序函数
16	my_sort(... , std::less<... >());
17	// 借助于值实参（即函数实参）传递进来的仿函数，来定义排序函数
18	my_sort(... , my_criterion);

作为非类型模板实参的仿函数

我们同样也可以通过非类型模板实参的形式来提供仿函数。然而，class类型的仿函数（更普遍而言，应该称为class类型的对象）将不能作为一个有效的非类型模板实参。如下面的代码就是无效的：

class MyCriterion
{
    public:
        bool operator() (SomeType const&, SomeType const&) const;
};

template<MyCriterion F>        // ERROR:MyCriterion 是一个class类型
void my_sort(... );

然而，我们可以让一个指向class类型对象的指针或者引用作为非类型实参，这也启发了我们编写出下面的代码：

class MyCriterion
{
    public:
        virtual bool operator() (SomeType const&, SomeType const&) const = 0;
};

class LessThan : public MyCriterion
{
    public:
        virtual bool operator() (SomeType const&, SomeType const&) const;
};

template<MyCriterion& F>        // class类型对象的指针或引用
void sort(... );

LessThan order;
sort<order> (... );        // 错误：要求派生类到基类的转型
sort<(MyCriterion&)order>(... );        // 非类型模板实参所引用的必须是一个简单的名称（不能含有转型）

在上面这个例子中，我们的目的是为了在抽象基类中描述这种排序规则的接口，并且在非类型模板实参中使用该抽象类型。就我们的想法而言，我们是为了能够在派生类（如LessThan）中来特定地实现基类的这种接口（MyCriterion）。遗憾的是，C并不允许这种实现方法，在C中，借助于引用或者指针的非类型实参必须能够和参数类型精确匹配，从派生类到基类的转型是不允许的，而进行显式类型转换也会使实参无效，同样也是错误的。

结论：

class类型的仿函数并不适合以非类型模板实参的形式进行传递。
相反，函数指针（或者函数引用）却可以是有效的非类型模板实参。

函数指针的封装

本节主要介绍：把一个合法的函数嵌入一个接收class类型仿函数框架。
因此，我们可以定义一个模板，从而可以方便地嵌入这种函数：

#include <vector>
#include <iostream>
#include <cstdlib>

// 用于把函数指针封装成函数对象的封装类
template <int (*FP)() >
class FunctionReturningIntWrapper
{
    public:
        int operator() (){
            return FP();
        }
};

// 要进行封装的函数实例
int random_int()
{
    return std::rand();        // 调用标准的C函数
}

// 客户端，它使用由模板参数传递进来的函数对象类型
template <typename FO>
void initialize(std::vector<int>& coll)
{
    FO fo;        // 创建函数对象
    for(std::vector<int>::size_type i=0; i<coll.size(); ++i){
        coll[i] = fo();        // 调用由函数对象表示的函数
    }
}

int main()
{
    // 创建含有10个元素的vector
    std::vector<int> v(10);

    // 用封装函数来（重新）初始化vector的值
    initialize<FunctionReturningIntWrapper<random_int> > (v);

    // 输出vector中元素的值
    for(std::vector<int>::size_type i=0; i<v.size(); ++i){
        std::cout << "coll[" << i << "]:" << v[i] << std::endl;
    }
}

其中位于initialize()内部的表达式:

1	FunctionReturningIntWrapper<random_int>

封装了函数指针random_int，于是我们可以把

1	FunctionReturningIntWrapper<random_int>

作为一个模板类型参数传递给initialize函数模板。

注意:我们不能把一个具有C链接的函数指针直接传递给类模板FunctionReturningIntWrapper。例如：

1	initialize<FunctionReturningIntWrapper<std::rand> > (v);

可能就会是错误的，因为std::rand()是一个来自C标准库的函数（因此也就具有C链接）。然而，我们可以引入一个typedef，从而就可以使一个函数指针类型具有合适的链接：

// 针对具有C链接的函数指针的类型
extern "C" typedef int (*C_int_FP) ();

// 把函数指针封装成函数对象的类
template <C_int_FP FP>
class FunctionReturningIntWrapper
{
    public:
        int operator() (){
            return FP();
        }
};

分析一个仿函数的类型

在我们的框架中，我们只是处理class类型的仿函数，并且要求框架可以提供以下这些于仿函数相关的属性：

仿函数参数的个数（作为一个成员枚举常量NumParams）
仿函数每个参数的类型（通过成员typedef Param1T、Param2T、Param3T来表示）
仿函数的返回类型（通过一个成员typedef ReturnT来表示）

例如，我们可以这样编写PersonSortCriterion，使之适合我们前面的框架：

class PersonSortCriterion
{
    public:
        enum { NumParams = 2 };
        typedef bool ReturnT;
        typedef Person const& Param1T;
        typedef Person const& Param2T;
        bool operator() (Person const& p1, Person const& p2) const {
            // 返回p1是否“小于”p2
            ....
        }
};

对于没有副作用的仿函数，我们通常把它称为纯仿函数。
例如，通常而言，排序规则就必须是纯仿函数，否则的话排序操作的结果将会是毫无意义的。

访问参数的类型

仿函数可以具有任意数量的参数。我们期望能够编写一个类型函数，对于一个给定的仿函数类型和一个常识N，可以给出该仿函数第N个参数的类型：

#include "ifthenelse.hpp"

template <typename F, int N>
class UsedFunctorParam;

template<typename F, int N>
class FunctorParam
{
    private:
        // 当N值大于仿函数的参数个数时的类型：FunctorParam<F, N>::Type的类型为私有class类型
        // 不使用FunctorParam<F, N>::Type的值为void的原因，是因为void自身会有很多限制，如函数不能接受类型为void的参数
        class Unused
        {
            private:
                // 这种类型的对象不能被创建
                class Private {}
            public:
                typedef Private Type;
        };
    public:
        typedef typename IfThenElse<F::NumParams>=N,
                                                    UsedFunctorParam<F, N>,
                                                    Unused>::ResultT::Type
                    Type;
};

template <typename F>
class UsedFunctorParam<F, 1>
{
    public:
        typedef typename F::Param1T Type;
};

UsedFunctorParam是我们引入的一个辅助模板，对于每一个特定的N值，都需要对该模板进行局部特化，下面使用宏来实现：

#define FunctorParamSpec(N)                                                    \
            template<typename F>                                                \
            class UsedFunctorParam<F, N>{                                    \
                public:                                                                    \
                    typedef typename F::Param##N##T Type;            \
            }
...
FunctorParamSpec(2);
FunctorParamSpec(3);
...
FunctorParamSpec(20);

#undef FunctorParamSpec

封装函数指针

上面一小节，我们借助于typedef的形式，是仿函数类型能够支持某些内省。然而，由于要实现这些内省的约束，函数指针不再适用于我们的框架。我们可以通过封装函数指针来绕过这种限制。我们可以开发一个小工具，它能够封装最多具有2个参数的函数（封装含有多个参数的函数的原理和做法是一样的）。

接下来给出的解释方案将会涉及到2个组件：类模板FunctionPtr，它的实例就是封装函数指针的仿函数类型；重载函数模板func_ptr，它接收一个函数指针为参数，然后返回一个相应的、适合该框架的仿函数。其中，类模板FunctionPtr将由返回类型和参数类型进行参数化：

1	template<typename RT, typename P1 = void, typename P2 = void>
2	class FunctionPtr;

用void值来替换一个参数意味着：该参数实际上并没有提供。因此，我们的模板能够处理仿函数调用实参个数不同的情况。
因为我们需要封装的是函数指针，所以我们需要有一个工具，它能够根据参数的类型，来创建函数指针类型。我们通过下面的局部特化来实现这个目的：

// 基本模板，用于处理参数个数最大的情况：
template <typename RT, typename P1 = void,
                                    typename P2 = void,
                                    typename P3 = void>
class FunctionPtrT
{
    public:
        enum { NumParams = 3 };
        typedef RT (*Type)(P1, P2, P3);
};

// 用于处理两个参数的局部特化
template <typename RT, typename P1,
                                    typename P2>
class FunctionPtrT<RT, P1, P2, void>
{
    public:
        enum { NumParams = 2 };
        typedef RT (*Type)(P1, P2);
};

// 用于处理一个参数的局部特化
template<typename RT, typename P1>
class FunctionPtrT<RT, P1, void, void>
{
    public:
        enum { NumParams = 1 };
        typedef RT (*Type)(P1);
};

// 用于处理0个参数的局部特化
template<typename RT>
class FunctionPtrT<RT, void, void, void>
{
    public:
        enum { NumParams = 0 };
        typedef RT (*Type)();
};

你会发现，我们还使用了上面这个（相同的）模板来计算参数的个数。

对于上面这个仿函数类型，它把它的参数传递给所封装的函数指针。然而，传递一个函数调用实参是可能会产生副作用的：如果相应的参数属于class类型（而不是一个指向class类型的引用），那么在传递的过程中，将会调用该class类型的拷贝构造函数。

为了避免这个（调用拷贝构造函数）额外的开销，我们需要编写一个类型函数；在一般情况下，该类型函数不会改变实参的类型，而当参数是属于class类型的时候，它会产生一个指向该class类型的const引用。借助于在前面章节开发的TypeT模板和熟知的IfThenElse功能模板，我们可以这样准确地实现这个类型函数：

#include "ifthenelse.hpp"
#include "typet.hpp"
#include "typeop.hpp"

// 对于class类型，ForwardParamT<T>::Type是一个常引用
// 对于其他的所有类型，ForwardParamT<T>::Type是普通类型
// 对于void类型，ForwardParamT<T>::Type是一个哑类型（Unused）
template<typename T>
class ForwardParamT
{
    public:
        typedef typename IfThenElse<TypeT<T>::IsClassT,
                                                    typename TypeOp<T>::RefConstT,
                                                    typename TypeOp<T>::ArgT
                                                    >::ResultT
                    Type;
};
template<>
class ForwardParamT<void>
{
    private:
        class Unused { };
    public:
        typedef Unused Type;
};

我们发现这个模板和前面的RParam模板非常相似，唯一的区别在于：在此我们需要把void类型（我们在前面已经说明，void类型是用于代表那些没有提供参数的类型）映射为一个类型，而且该类型必须是一个有效的参数类型。

现在，我们已经能够定义FunctionPtr模板了。另外，由于我们事先并不知道FunctionPtr究竟会接收多少个参数，所以在下面的代码中，我们针对不同个数的参数（但在此我们最多只是针对3个参数），都重载了函数调用运算符：

// functors/functionptr.hpp

#include "forwardparam.hpp"
#include "functionptrt.hpp"

template<typename RT, typename P1 = void,
                                    typename P2 = void,
                                    typename P3 = void>
class FunctionPtr
{
    private:
        typedef typaname FunctionPtrT<RT, P1, P2, P3>::Type FuncPtr;
        // 封装的指针
        FuncPtr fptr;
    public:
        // 使之适合我们的框架
        enum { NumParams = FunctionPtrT<RT, P1, P2, P3>::NumParams };
        typedef RT ReturnT;
        typedef P1 Param1T;
        typedef P2 Param2T;
        typedef P3 Param3T;

        // 构造函数：
        FunctionPtr(FuncPtr ptr) : fptr(ptr) { }

        // "函数调用":
        RT operator() (){
            return fptr();
        }

        RT operator() (typename ForwardParamT<P1>::Type a1) {
            return fptr(a1);
        }

        RT operator() (typename ForwardParamT<P1>::Type a1,
                            typename ForwardParamT<P2>::Type a2) {
            return fptr(a1, a2);
        }

        RT operator() (typename ForwardParamT<P1>::Type a1,
                            typename ForwardParamT<P2>::Type a2,
                            typename ForwardParamT<P3>::Type a3) {
            return fptr(a1, a2, a3);
        }
};

该类模板可以实现所期望的功能，但如果直接使用该模板，将会比较繁琐。为了使之具有更好的易用性，我们可以借助模板的实参演绎机制，实现每个对应的（内联的）函数模板：

#include "functionptr.hpp"

template <typename RT> inline
FunctionPtr<RT> func_ptr (RT (*fp) () )
{
    return FunctionPtr<RT>(fp);
}

template <typename RT, typename P1> inline
FunctionPtr<RT, P1> func_ptr (RT (*fp) (P1) )
{
    return FunctionPtr<RT, P1>(fp);
}

template <typename RT, typename P1, typename P2> inline
FunctionPtr<RT, P1, P2> func_ptr (RT (*fp) (P1, P2) )
{
    return FunctionPtr<RT, P1, P2>(fp);
}

template <typename RT, typename P1, typename P2, typename P3> inline
FunctionPtr<RT, P1, P2, P3> func_ptr (RT (*fp) (P1, P2, P3) )
{
    return FunctionPtr<RT, P1, P2, P3>(fp);
}

至此，剩余的工作就是编写一个使用这个（高级）模板工具的实例程序了。如下所示：

#include <iostream>
#include <string>
#include <typeinfo>
#include "funcptr.hpp"

double seven()
{
    return 7.0;
}

std::string more()
{
    return std::string("more");
}

template <typename FunctorT>
void demo(FunctorT func)
{
    std::cout << "Functor returns type "
                << typeid(typename FunctorT::ReturnT).name() << '\n'
                << "Functor returns value "
                << func() << '\n';
}

int main()
{
    demo(func_ptr(seven));
    demo(func_ptr(more));
}

C++ Template By David Vandevoorde还介绍了函数对象组合和和值绑定的相关知识点及其实现。函数对象组合通过组合两个或多个仿函数，来实现多个仿函数功能的组合，完成较为复杂的操作；而值绑定通过对一个具有多个参数的仿函数，把其中一个参数绑定为一个特定的值。

@Reference

Advanced C++ Template Techniques:An Introduction to Meta-Programming for Scientific Computing
C++ Template By David Vandevoorde

1	template <typename T>
2	inline T const& tmax(T const& a, T const& b)
3	{
4	return a < b ? b: a;
5	}

1	#include <cassert>
2	#include <vector>
3
4	template <typename T>
5	class Stack {
6	private:
7	std::vector<T> elems; // elements
8
9	public:
10	void push(T const& elem); // push element
11	void pop(); // pop element
12	T const& top() const; // return top element
13	bool empty() const { // return whether the stack is empty
14	return elems.empty();
15	}
16	};
17
18	template <typename T>
19	void Stack<T>::push(T const& elem) {
20	elems.push_back(elem); // append copy of passed elem
21	}
22
23	template <typename T>
24	void Stack<T>::pop() {
25	assert(!elems.empty());
26	elems.pop_back(); // remove last element
27	}
28
29	template <typename T>
30	T const& Stack<T>::top() const {
31	assert(!elems.empty());
32	return elems.back(); // return copy of last element
33	}

1	template <typename T>
2	class Stack
3	{
4	...
5	void push(T const& elem)
6	{
7	elems.push_back(elem);
8	}
9	...
10	};

1	template<typename T, typename M> class test{
2	T i;
3	M m;
4	};
5	template<typename M> class test<bool, M>{
6	int i;
7	};

1	template<typename T> class test{
2	T i;
3	};
4	template<typename T> class test<T*>{
5	T i;
6	};
7	template<typename T> class test<const T*>{
8	T i;
9	};

1	template <typename T, typename CONT = std::vector<T> >
2	class Stack
3	{
4	};
5
6	template <typename T1, typename T2 = int>
7	class Sample
8	{
9	};

1	template <typename T, int MAXSIZE>
2	class Stack
3	{
4	};
5	// 使用
6	Stack<int, 20> int20Stack; // 可以存储20个int元素的栈
7	Stack<int, 40> int40Stack; // 可以存储40个int元素的栈

1	template <typename T, int VAL>
2	T addValue(T const& x)
3	{
4	return x + VAL;
5	}

1	template <char const* name>
2	class MyClass
3	{
4	};
5	MyClass<"hello"> x; // ERROR:不允许使用字符文字"hello"
6	//另外，你也不能使用全局指针作为模板参数：
7	template <char const* name>
8	class MyClass
9	{
10	...
11	};
12	char const* s = "hello";
13	MyClass<s> x; // s是一个指向内部链接对象的指针
14	//然而，你可以这样使用：
15	template <char const* name>
16	class MyClass
17	{
18	...
19	};
20	extern char const s[] = "hello";
21	MyClass<s> x; // OK
22	//全局字符数组s由“hello”初始化，是一个外部链接对象。

1	template <typename T>
2	class MyClass
3	{
4	// 这里的typename被用来说明：T::SubType是定义于类T内部的一种类型
5	typename T::SubType* ptr;
6	...
7	};

1	template <typename T>
2	class Base
3	{
4	public:
5	void exit();
6	};
7
8	template <typename T>
9	class Derived : Base<T> // 模板基类
10	{
11	public:
12	void foo()
13	{
14	exit(); // 调用外部的exit()或者出现错误，而不会调用模板基类的exit()
15	}
16	};

1	template <typename T>
2	class Stack
3	{
4	...
5	template <typename T2>
6	Stack<T>& operator= (Stack<T2> const&);
7	};

1	template <typename T,
2	template <typename ELEM,
3	typename ALLOC = std::allocator<ELEM> >
4	class CONT = std::deque >
5	class Stack
6	{
7	...
8	};

1	template <typename T, int N, int M>
2	T const* max (T const (&a)[N], T const (&b)[M])
3	{
4	return a < b ? b : a;
5	}

1	template <typename T1, typename T2> // 基本的类模板
2	class MyClass
3	{
4	...
5	};
6	template<> // 显式特化
7	class MyClass<std::string, float>
8	{
9	...
10	};

1	template <typename T> // 基本的类模板
2	class MyClass<T, T>
3	{
4	...
5	};
6	template<typename T> // 局部特化
7	class MyClass<bool, T>
8	{
9	...
10	};

1	// 类模板
2	template <typename T>
3	class List // 作为名字空间作用域的类模板
4	{
5	public:
6	template <typename T2>
7	List(List<T2> const&); // 成员函数模板（构造函数）
8	};
9
10	template <typename T>
11	template <typename T2>
12	List<T>::List(List<T2> const& b){} // 位于类外部的成员函数模板定义
13
14	// 位于外部名字空间作用域的函数模板
15	template <typename T>
16	int length(List<T> const&);
17
18	// 联合（Union）模板，往往被看作类模板的一种
19	template <typename T>
20	union AllocChunk
21	{
22	T object;
23	usigned char bytes[sizeof(T)];
24	};

1	template <int I>
2	class CupBoard
3	{
4	void open();
5	class Shelf;
6	static double total_weight;
7	...
8	};
9
10	template <int I>
11	void CupBoard<I>::open(){ ... }
12
13	template <int I>
14	class CupBoard<I>::Shelf { ... };
15
16	template <int I>
17	double CupBoard<I>::total_weight = 0.0;

1	template <typename T>
2	class Dynamic
3	{
4	public:
5	virtual ~Dynamic(); // ok：类模板的普通成员函数，每个Dynamic只对应一个析构函数
6	template <typename T2>
7	virtual void copy(T2 const&); // 错误，在确定Dynamic<T>实例的时候，并不知道copy()的个数
8	};

1	int C;
2	class C; // 正确：类名称和非类名称位于不同的名字空间
3
4	int X;
5	template <typename T>
6	class X; //Error: Redefinition of 'X' as different kind of symbol
7
8	struct S;
9	template <typename T>
10	class S; //Error：Redefinition of 'S' as different kind of symbol

1	extern "C++" template <typename T>
2	void normal(); // 这是缺省情况，上面的链接规范可以不写
3
4	extern "C" template <typename T> // ERROR: Templates must have C++ linkage
5	void invalid();
6
7	extern "Xroma" template <typename T>
8	void xroma_link(); // 非标准的，当某些编译器将来可能支持写Xroma语言的链接兼容性

1	template <int buf[5]> class Lexer; // buf实际上是一个int*类型
2	template <int* buf> class Lexer; // 正确：这是上面的重新声明

1	template <typename RT, typename T>
2	inline RT func(T const &){ ... }
3
4	template <typename T, typename RT>
5	inline RT func1(T const &){ ... }
6
7	int main()
8	{
9	double value1 = func<double>(-1); // double 显式指定RT类型，-1实参演绎T类型
10	double value2 = func1<int, double>(-1); // 要显式指定RT的类型，必须同时显式指定它前面的类型T
11	}

1	template <typename T> class List
2	{
3	...
4	};
5
6	typedef struct
7	{
8	double x, y, z;
9	}Point;
10
11	typedef enum { red, green, blue } *ColorPtr;
12
13	int main()
14	{
15	struct Association
16	{
17	int* p;
18	int* q;
19	};
20
21	// 错误：模板实参中使用了局部类型
22	List<Association*> error1;
23
24	// 错误：模板实参中使用了未命名的类型，因为typedef定义的是*ColorPtr，并非ColorPtr
25	List<ColorPtr> error2;
26
27	// 正确：通过使用typedef定义的未命名类型
28	List<Point> ok;
29	}

1	template <typename T>
2	int f(T)
3	{
4	return 1;
5	}
6
7	template <typename T>
8	int f(T*)
9	{
10	return 2;
11	}

1	template<typename T>
2	class S
3	{
4	public:
5	void info()
6	{
7	std::cout << "generic (S<T>::info() \n)";
8	}
9	};
10
11	template<>
12	class S<void>
13	{
14	public:
15	void msg()
16	{
17	std::cout << "fully specialized (S<void>::msg()) \n";
18	}
19	};

1	template<typename T>
2	class S;
3
4	template<>
5	class S<char**>
6	{
7	public:
8	void print() const;
9	};
10
11	// 下面的定义不能使用template<>前缀
12	void S<char**>::print() const
13	{
14	std::cout << "pointer to pointer to char \n";
15	}

1	template<typename T>
2	class Outer // (1)
3	{
4	public:
5	template<typename U>
6	class Inner // (2)
7	{
8	private:
9	static int count; // (3)
10	};
11	static int code; // (4)
12	void print() const // (5)
13	{
14	std::cout << "generic";
15	}
16	};
17
18	template<typename T>
19	int Outer<T>::code = 6; // (6)
20
21	template<typename T>
22	template<typename U>
23	int Outer<T>::Inner<U>::count = 7; // (7)
24
25	template<>
26	class Outer<bool> // (8)
27	{
28	public:
29	template<typename U>
30	class Inner // (9)
31	{
32	private:
33	static int count; // (10)
34	};
35	void print() const {} // (11)
36	};

1	template<>
2	int Outer<void>::code = 12;
3
4	template<>
5	void Outer<void>::print() const
6	{
7	std::cout << "Outer<void>";
8	}

1	template<>
2	int Outer<void>::code;
3
4	template<>
5	void Outer<void>::print() const;