0%

Math Formula Theorem (常用数学公式定理)

Posted on Edited on In

记录一些常用到的数学公式、定理以及分析方法.

Procrustes Analysis(普氏分析)

前言

选取N幅同类目标物体的二维图像，并法标注轮廓点，这样就得到训练样本集

Ω={X1,X2,⋯ ,XN}\Omega = \{X_1, X_2, \cdots, X_N\}

由于图像中目标物体的形状和位置存在较大偏差，因此所得到的数据并不具有仿射不变性，需要对其进行归一化处理。这里采用Procrustes分析方法对样本集中的所有形状集合进行归一化。形状和位置的载体还是样本点的空间坐标。

定义

普氏分析法是一种用来分析形状分布的方法。数学上来讲，就是不断迭代，寻找标准形状(canonical shape)，并利用最小二乘法寻找每个样本形状到这个标准形状的仿射变化方式。

本书中，两个形状的归一化过程（一个形状为canonical shape，另一个为样本形状）：

  1. 求每个样本点i(i=1,2..,n)i(i=1,2..,n)在N幅图像中的均值

(xˉi,yˉi)=(1N∑j=1Nxji,1N∑j=1Nyji)(\bar x_i, \bar y_i) = \bigg(\frac{1}{N}\sum_{j=1}^Nx_{ji}, \frac{1}{N}\sum_{j=1}^Ny_{ji}\bigg)

  1. 对所有形状的大小进行归一化，即将每个样本点减去其对应均值

(xi′,yi′)=(xi−xˉi,yi−yˉi)(x_i', y_i') = (x_i - \bar x_i, y_i - \bar y_i)

  1. 根据去中心化数据，计算每幅图像中形状的重心，对于第ii幅图像，其重心为

(xˉi,yˉi)=(1n∑j=1nxji,1n∑j=1nyji)(\bar x_i, \bar y_i) = \bigg(\frac{1}{n}\sum_{j=1}^nx_{ji}, \frac{1}{n}\sum_{j=1}^ny_{ji}\bigg)

  1. 根据重心和角度，将标准和样本形状对齐在一起，使得两个形状的普氏距离最小，下式为普氏距离定义

Pd2=∑i=1n[(xi1−xi2)2+(yi1−yi2)2]P_d^2 = \sum_{i=1}^n[(x_{i1} - x_{i2})^2 + (y_{i1} - y_{i2})^2]

这个第44步的具体做法，不断迭代以下过程：

  1. 通过计算每幅图像中所有归一化样本点的平均值得到每个图像的标准形状canonical shape。
  2. 利用最小二乘法求每个图像中样本形状到标准形状的旋转角度。根据普氏距离的定义，也就是求

min⁡a,b∑i=1n∣∣[a−bba][xiyi]−[cxcy]∣∣2\min_{a,b}\sum_{i=1}^n\bigg|\bigg|\begin{bmatrix}a & -b\\ b & a\end{bmatrix}\begin{bmatrix}x_i \\ y_i\end{bmatrix}-\begin{bmatrix}c_x\\c_y\end{bmatrix}\bigg|\bigg|^2

其中的aa和bb表示仿射变换里旋转变化的参数：

[a−bba]=[kcos(θ)−ksin(θ)ksin(θ)kcos(θ)]\begin{bmatrix}a & -b\\ b & a\end{bmatrix} = \begin{bmatrix}kcos(\theta)& -ksin(\theta) \\ ksin(\theta) & kcos(\theta)\end{bmatrix}

对上式求偏导数，可以得到所求的a和b：

[ab]=1Σi(xi2+yi2)∑i=1n[xicx+yicyxicy−yicx]\begin{bmatrix}a \\ b\end{bmatrix} = \frac{1}{\Sigma_i(x_i^2 + y_i^2)}\sum_{i=1}^n\begin{bmatrix}x_ic_x + y_ic_y \\ x_ic_y - y_ic_x\end{bmatrix}

  1. 根据旋转参数，对样本形状做旋转变化，得到和标准形状对齐的新的形状

[x′y′]=[a−bba][xy]\begin{bmatrix}x' \\ y'\end{bmatrix} = \begin{bmatrix}a & -b \\ b & a\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}

  1. 重复以上步骤，直到达到指定循环次数或者前后两次迭代之间canonical shape的绝对范数满足一定阈值

Procrustesanalysis的作用可以看作是一种对原始数据的预处理，目的是为了获取更好的局部变化模型作为后续模型学习的基础。如下图所示，每一个人脸特征点可以用一种单独的颜色表示；经过归一化变化，人脸的结构越来越明显，即脸部特征簇的位置越来越接近他们的平均位置；经过一系列迭代，尺度和旋转的归一化操作，这些特征簇变得更加紧凑，它们的分布越来越能表达人脸表情的变化。【剔除刚性部分、保留柔性部分】
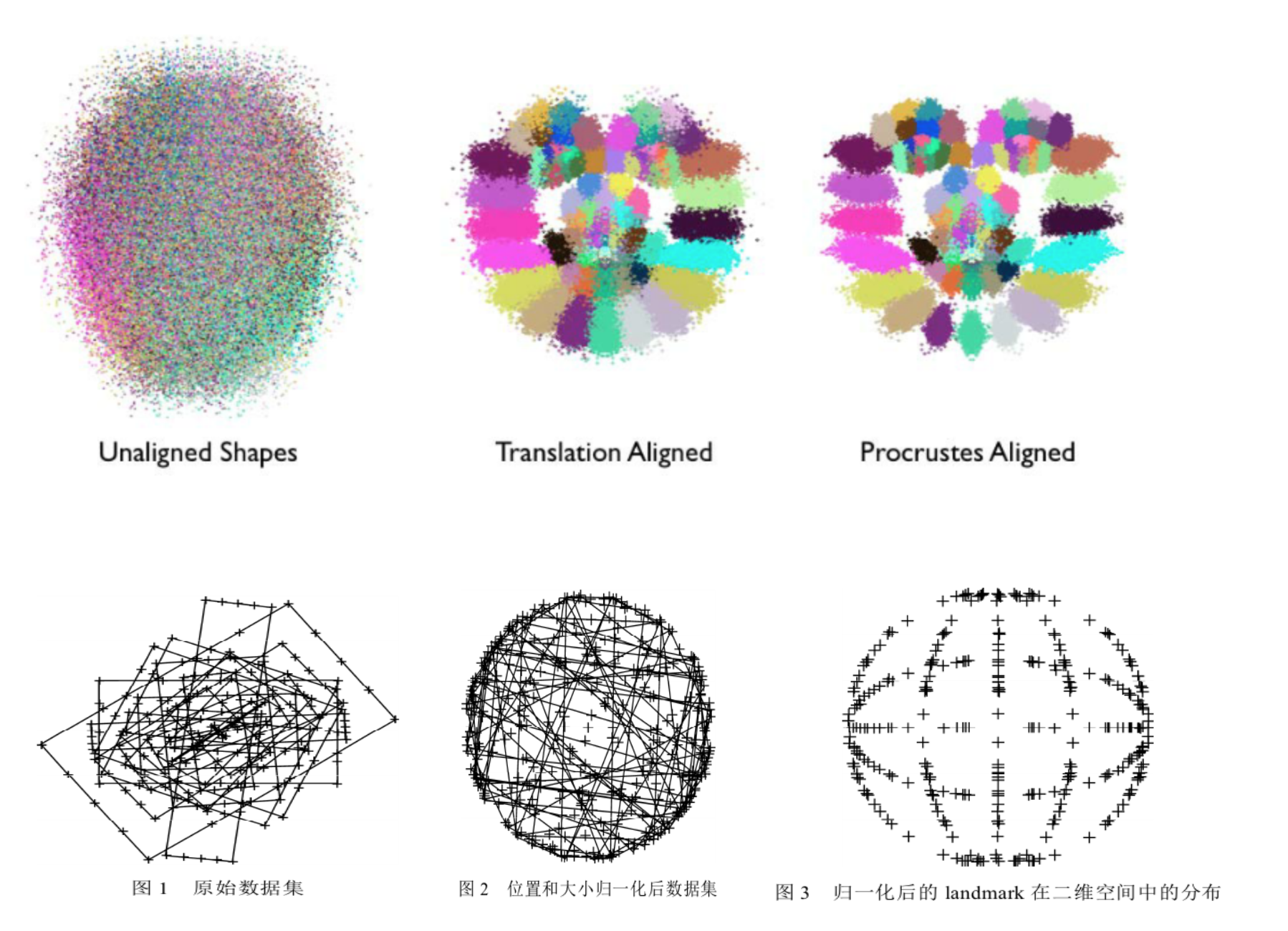
procrustes-analysis-sample
上图为不同大小、不同长宽比的矩形，经过归一化过程后，各个样本点分布服从一定概率分布趋势。

具体代码实现：

1
/**
2
@函数：Mat shape_model::procrustes(const Mat &X,
3
                                  const int itol,constfloat ftol)
4
@矩阵X：2n*N维矩阵，即有N副图像，每幅图像有n个特征点（2n是因为x和y坐标）
5
@Itol：迭代次数
6
@Ftol：求绝对范数的阈值
7
@返回值：矩阵P，存放对齐后的形状坐标
8
**/
9
Mat shape_model::procrustes(const Mat &X,const int itol,const float ftol)
10
{
11
  /* X.cols:特征点个数，X.rows: 图像数量*2 */
12
  int N = X.cols,n = X.rows/2; 
13
14
  //remove centre of mass
15
  Mat P = X.clone();
16
  for(int i = 0; i < N; i++)
17
  {
18
    /*取X第i个列向量*/
19
    Mat p = P.col(i);
20
    float mx = 0,my = 0;
21
    for(int j = 0; j < n; j++)
22
    {
23
        mx += p.fl(2*j);
24
        my += p.fl(2*j+1);
25
    }
26
    /*分别求图像集，2维空间坐标x和y的平均值*/
27
    mx /= n;
28
    my /= n;
29
    /*对x,y坐标去中心化*/
30
    for(int j = 0; j < n; j++)
31
    {
32
        p.fl(2*j) -= mx; 
33
        p.fl(2*j+1) -= my;
34
    }
35
  }
36
  //optimise scale and rotation
37
  Mat C_old;
38
  for(int iter = 0; iter < itol; iter++)
39
  {   
40
    /*计算（含n个形状）的重心*/  
41
    Mat C = P*Mat::ones(N,1,CV_32F)/N; 
42
    /*C为2n*1维矩阵，含n个重心，对n个重心归一化处理*/
43
    normalize(C,C);
44
    if(iter > 0)
45
    {
46
      if(norm(C,C_old) < ftol)//norm:求绝对范数，小于阈值，则退出循环
47
        break;
48
    }
49
    C_old = C.clone();
50
    for(int i = 0; i < N; i++)
51
    {
52
      //求当前形状与归一化重心之间的旋转角度，即上式a和b
53
      Mat R = this->rot_scale_align(P.col(i),C); 
54
      for(int j = 0; j < n; j++)
55
      {
56
        float x = P.fl(2*j,i),y = P.fl(2*j+1,i);
57
        /*仿射变化*/
58
        P.fl(2*j  ,i) = R.fl(0,0)*x + R.fl(0,1)*y;
59
        P.fl(2*j+1,i) = R.fl(1,0)*x + R.fl(1,1)*y;
60
      }
61
    }
62
  }
63
return P;
64
}

Lagrange Multipliers (拉格朗日乘算子)

Poisson Theorem (泊松定理)

泊松论文